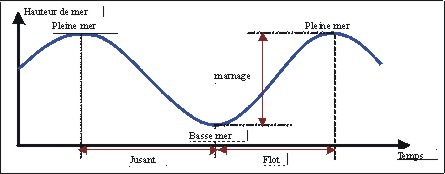
Figure 3 : Courbe de marée
Il existe d’autres types de marées que les marées océaniques. Ainsi, les marées atmosphériques sont des déplacements ondulatoires des masses d’air de notre atmosphère et les marées terrestres sont des déformations périodiques de la croûte terrestre. Ces deux marées se font au même rythme que celui des marées océaniques et sont aussi générées par le mouvement des astres. Mais il existe d’autres marées qui ne sont pas d’origine astronomique. Les seiches apparaissent dans des bassins de géométrie particulière et sont générées par le vent ou les variations de pression atmosphérique qui engendrent des oscillations de la surface (ce phénomène a souvent lieu dans des lacs). La marée radiationnelle provient de la dilatation des eaux de surface des océans due aux alternances jour/nuit cycliques qui réchauffent ou refroidissent l’eau. Les marées météorologiques sont créées par les variations périodiques de vents alternatifs (tels la mousson ou les vents solaires) ou par les variations de pression atmosphérique. Cependant, le but de notre travail étant l’étude des marées océaniques, nous désignerons dans la suite la marée océanique par le terme de ‘marée’. Dans le cas contraire, nous préciserons le type de marée.
Il est particulièrement important de faire ressortir la principale caractéristique de la marée : la rigoureuse périodicité du phénomène. En effet, le mouvement des astres étant la cause de la marée et leurs déplacements périodiques étant parfaitement connus, la périodicité des élévations du niveau des océans due à la marée est, elle aussi, connue. Comme nous le verrons plus loin, cette caractéristique permet l’analyse harmonique de la marée.

Figure 3 : Courbe de marée
 que nous désignerons plus simplement par
que nous désignerons plus simplement par 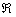 .
.
L’origine de  est
le centre T de la Terre et ses axes ont des directions fixes par rapport
aux étoiles supposées fixes. L’axe en z est pris comme étant
l’axe des pôles. Plaçons-nous dans ce repère
est
le centre T de la Terre et ses axes ont des directions fixes par rapport
aux étoiles supposées fixes. L’axe en z est pris comme étant
l’axe des pôles. Plaçons-nous dans ce repère 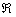 lié à la Terre et déterminons le mouvement d’une particule
P de masse m à la surface de la Terre, soumise aux
forces d’origines terrestre et astronomique. Considérons les hypothèses
simplificatrices suivantes :
lié à la Terre et déterminons le mouvement d’une particule
P de masse m à la surface de la Terre, soumise aux
forces d’origines terrestre et astronomique. Considérons les hypothèses
simplificatrices suivantes :
 reste constant en direction, en sens (axe des pôles fixe) et en intensité
(vitesse de rotation constante) ;
reste constant en direction, en sens (axe des pôles fixe) et en intensité
(vitesse de rotation constante) ;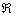 est
animé :
est
animé :
 d’un point P de masse m à la surface de la Terre dans
d’un point P de masse m à la surface de la Terre dans  :
:
 (3.1)
(3.1)
avec :
 : le champ d’attraction terrestre
;
: le champ d’attraction terrestre
; : le vecteur de T à
P ;
: le vecteur de T à
P ; : la vitesse relative dans
: la vitesse relative dans  ;
;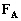 : la force d’attraction astronomique.
: la force d’attraction astronomique.Le terme qui nous intéresse plus
particulièrement est  : il représente la force génératrice des marées.
Cette force génératrice est donc l’expression d’un différentiel
entre la force astronomique qui s’applique sur la particule P de la part
des astres qui tournent autour de la Terre diminuée de la force
astronomique qui s’applique au centre de la Terre de la part de ces mêmes
astres.
: il représente la force génératrice des marées.
Cette force génératrice est donc l’expression d’un différentiel
entre la force astronomique qui s’applique sur la particule P de la part
des astres qui tournent autour de la Terre diminuée de la force
astronomique qui s’applique au centre de la Terre de la part de ces mêmes
astres.
 (3.2)
(3.2)
avec :
 : le vecteur de direction la ligne
passant par P1 et P2, de sens P1
vers P2 et de module la distance de P1
à P2.
: le vecteur de direction la ligne
passant par P1 et P2, de sens P1
vers P2 et de module la distance de P1
à P2.
avec :
Dans le degré d’approximation nécessaire au calcul des marées, seuls la Lune et le Soleil ont une influence sur la Terre (le Soleil a une très grande masse et la Lune est proche de la Terre). Les autres planètes ou étoiles qui entourent la Terre sont trop éloignées ou de masses trop faibles pour être prises en considération. La seule résultante newtonienne qui agit sur la Terre n’est due qu’au Soleil et à la Lune dans l’étude des marées.
Considérons les deux astres, Terre et Lune ou Terre et Soleil. Etant donné que les distances les séparant sont de plusieurs ordres de grandeur supérieurs à leur diamètre respectif (cf. Tableau 2), nous pouvons considérer que les astres sont ponctuels et donc que la loi de Newton peut leur être appliquée. Ainsi :
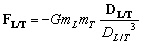 ;
; ;
; le vecteur allant du centre S du
Soleil au centre T de la Terre ;
le vecteur allant du centre S du
Soleil au centre T de la Terre ; le vecteur allant du centre L de
la Lune au centre T de la Terre.
le vecteur allant du centre L de
la Lune au centre T de la Terre.| Astre |
Terre/Astre (km) |
(km) |
Masse Terre |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 2 : Caractéristiques de la Lune et du Soleil par rapport à la Terre
D’après le paragraphe 3.3.1, la force génératrice des marées qui s’applique en un point P de masse unitaire appartenant à la surface océanique, est égale à la différence des champs d’attraction des astres en ce point et au centre T de la Terre. En considérant tous les astres k qui gravitent autour de la Terre, nous déduisons de (3.2) la force de génération des marées :
 (3.3)
(3.3)
avec :
Dans (3.3), en ne considérant qu’un
seul astre k, Rk et uk ne dépendent
que de la position de la Terre et de l’astre perturbateur. Par contre rk
et vk dépendent de la position de la particule
P de masse mk qui subit la force génératrice
des marées. C’est pourquoi le terme 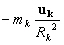 représente la force d’attraction exercée sur une masse mk
placée au centre de la Terre car elle est indépendante de
la position. Au contraire, le terme
représente la force d’attraction exercée sur une masse mk
placée au centre de la Terre car elle est indépendante de
la position. Au contraire, le terme  représente la force d’attraction sur la particule P de masse mk
dépendant de la position de P.
représente la force d’attraction sur la particule P de masse mk
dépendant de la position de P.

Figure 4 : Direction des forces gravitationnelles
par les interactions Terre/astre
La Terre, soumise à la force d’attraction gravitationnelle exercée par la Lune ou le Soleil, subit donc une accélération dirigée vers cet astre qui engendre une force d’inertie, la force centrifuge, appliquée en chaque point de la Terre. Pour une particule située au centre de la Terre, la force centrifuge s’oppose exactement à la force gravitationnelle. Cependant, ailleurs qu’au centre il n’y a pas équilibre. La force gravitationnelle varie avec le carré de la distance séparant un point de la Terre avec l’astre perturbateur. La Terre et la Lune (ou la Terre et le Soleil) ont un mouvement de translation circulaire, c’est pourquoi, la force centrifuge, reste la même en tout point du globe [Dronkers, 1964]. La force différentielle est la force génératrice des marées.
Soit A1 et A3 deux points de (TC) et A2 et A3 deux points de (PC) construits tels que :

Donc nous avons par construction :
CP’=CA4, CA3=CA2, CA1=CP=rk,
et par le théorème de Thalès :
 et
et  .
.
Comme 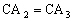 nous avons :
nous avons : 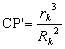 , d’où :
, d’où :
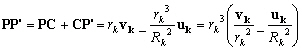
Aux coefficients multiplicateurs prêts 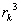 et mk, nous reconnaissons l’expression de la force génératrice
des marées données par (3.3). Ainsi, en tout point P de la
surface des océans, nous savons construire la force génératrice
des marées d’un astre k. Cet astre k de masse mk
exerce donc sur une particule P des océans qui est à
une distance Rk du centre est C de l’astre, une force
génératrice de marée :
et mk, nous reconnaissons l’expression de la force génératrice
des marées données par (3.3). Ainsi, en tout point P de la
surface des océans, nous savons construire la force génératrice
des marées d’un astre k. Cet astre k de masse mk
exerce donc sur une particule P des océans qui est à
une distance Rk du centre est C de l’astre, une force
génératrice de marée :
 (3.4)
(3.4)
Ce tracé se simplifie grâce à la règle de Proctor qui, supposant que l’astre k est à l’infini, entraîne que les arcs de cercle de construction sont des droites parallèles et donc que TP’=3TA1.
 décrit
entre l’axe centre de la Terre - centre de l’astre et l’axe centre de la
Terre - point P considéré.
décrit
entre l’axe centre de la Terre - centre de l’astre et l’axe centre de la
Terre - point P considéré. 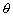 est appelé la distance zénithale de l’astre. Par la
règle de Proctor citée précédemment, nous avons
:
est appelé la distance zénithale de l’astre. Par la
règle de Proctor citée précédemment, nous avons
: 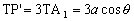 .
.

Figure 6 : Expression angulaire de
la force génératrice des marées
Par le théorème de Pythagore dans un triangle rectangle, nous avons :
 ,
,
d’où l’expression du module de la
force génératrice en fonction de  :
:
 (3.5)
(3.5)
Grâce à cette équation et à la méthode de tracé définit dans le paragraphe 3.3.2.3, nous pouvons définir la surface que prendrait une couche d’eau liquide recouvrant toute la Terre par l’influence d’un astre unique (cf. Figure 7, les proportions sont exagérées pour une meilleure visualisation). Cette surface est symétrique par rapport à l’axe des pôles d’une part et par rapport à l’axe centre de la Terre – centre de l’astre d’autre part. La surface est un ellipsoïde de révolution.
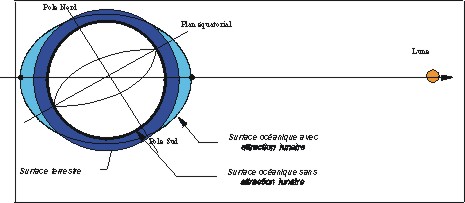
Figure 7 : Surface prise par un océan
global due à la force génératrice des marées
d’un astre unique

Ainsi, l’action de la Lune est deux fois plus importante que celle du Soleil malgré sa masse considérable : l’effet de distance est prépondérant.
Cependant ces forces différentielles sont infimes. Pour la Lune par exemple :

Par un calcul similaire nous avons pour le Soleil :

Ainsi, la composante verticale de ces forces différentielles ne modifie que très légèrement l’intensité de la pesanteur, de l’ordre du dix millionièmes, et leur composante horizontale en altère la direction, d’un angle de l’ordre du centième de seconde sexagésimale. Il est donc remarquable de noter que des forces aussi faibles conduisent à des variations du niveau de la mer aussi spectaculaires que celles que nous observons dans l’océan.

Dans les deux cas la force génératrice en P1 et en P2 est identique. La périodicité est donc la durée d’une demi rotation de l’axe perturbateur autour de la Terre. Dans ce cas, la force est dite semi-diurne pure.

Dans les deux cas la force génératrice en P1 et en P2 n’est plus identique. La force génératrice a toujours une périodicité semi-diurne, mais nous voyons apparaître des fluctuations diurnes dans les minima et les maxima de cette force. La périodicité reste semi-diurne mais avec des inégalités diurnes. Nous avons ainsi l’explication qualitative des variations semi-journalière et journalière constatées des élévations des océans et des mers le long des côtes terrestres.