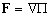 (4.6)
(4.6)
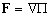 (4.6)
(4.6)
Avec 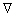 lopérateur nabla tel que dans les coordonnées cartésiennes
dun repère (Oxyz) :
lopérateur nabla tel que dans les coordonnées cartésiennes
dun repère (Oxyz) :
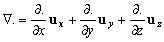
et 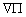 est
le gradient de P.
P
est une fonction scalaire.
est
le gradient de P.
P
est une fonction scalaire.
Le potentiel, défini à une constante près, est égal au travail queffectue la force pour déplacer une masse unité dun point vers un autre, indépendamment du chemin suivi. On montre quun champ dattraction créé par un point matériel P de masse m dérive dun potentiel P fonction de la distance r entre P et un point considéré :
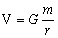 (4.7)
(4.7)
Dans le cas de létude des marées,
le potentiel qui dérive de la force génératrice des
marées est appelée potentiel générateur
des marées. Le gradient est un opérateur linéaire,
donc, dans le cas du système à trois corps qui nous intéresse
(Terre - Lune - Soleil), nous pouvons décomposer le potentiel astronomique
générateur total 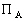 en la somme du potentiel générateur lunaire PL
et du potentiel générateur solaire PS.
Ainsi,
il suffit de déterminer PL,
par exemple, et PS
sen
déduit aisément. La somme du potentiel lunaire et du potentiel
solaire se nomme potentiel luni-solaire.
en la somme du potentiel générateur lunaire PL
et du potentiel générateur solaire PS.
Ainsi,
il suffit de déterminer PL,
par exemple, et PS
sen
déduit aisément. La somme du potentiel lunaire et du potentiel
solaire se nomme potentiel luni-solaire.
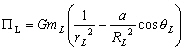 (4.8)
(4.8)
Dans le triangle TCP de la Figure 5, nous
avons la relation trigonométrique : 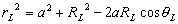 ,
ce qui permet décrire linverse de
,
ce qui permet décrire linverse de 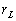 et le potentiel
et le potentiel 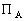 en fonction
de a, RL et
en fonction
de a, RL et 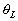 :
:
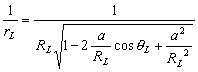 (4.9)
(4.9)
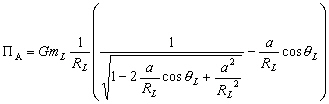 (4.10)
(4.10)
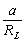 est petit devant 1. Dans le cas de la Lune,
est petit devant 1. Dans le cas de la Lune, 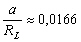 et dans le cas du Soleil
et dans le cas du Soleil 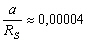 , donc
nous avons :
, donc
nous avons :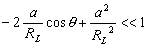 , et nous pouvons alors
décomposer (4.9) en une série entière de polynômes
de Legendre :
, et nous pouvons alors
décomposer (4.9) en une série entière de polynômes
de Legendre :
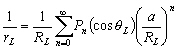 (4.11)
(4.11)
avec Pn les polynômes de Legendre définis par les relations :
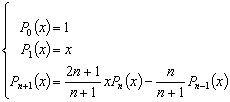 (4.12)
(4.12)
Cependant dans notre cadre détude,
le terme 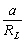 étant petit,
il entraîne une diminution très rapide de linfluence quantitative
des polynômes de Legendre avec lordre du développement. La
contribution du polynôme P2 représente environ
98% du potentiel lunaire total et une fraction encore plus importante du
potentiel solaire total [Le Provost, 1973]. Cest pourquoi, nous
nous limitons à lordre 2, limite de précision des mesures
in situ même si dans certains cas, le développement est utilisé
jusquà lordre 3 [Doodson, 1921; Le Provost, 1973]
Les quatre premiers polynômes de Legendre sécrivent alors
en fonction
étant petit,
il entraîne une diminution très rapide de linfluence quantitative
des polynômes de Legendre avec lordre du développement. La
contribution du polynôme P2 représente environ
98% du potentiel lunaire total et une fraction encore plus importante du
potentiel solaire total [Le Provost, 1973]. Cest pourquoi, nous
nous limitons à lordre 2, limite de précision des mesures
in situ même si dans certains cas, le développement est utilisé
jusquà lordre 3 [Doodson, 1921; Le Provost, 1973]
Les quatre premiers polynômes de Legendre sécrivent alors
en fonction 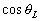 :
:
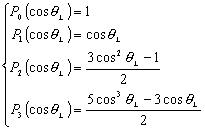 (4.13)
(4.13)
Ce qui nous permet après simplifications, puisque le potentiel est défini à une constante près, dexprimer le potentiel générateur lunaire à lordre 3 :
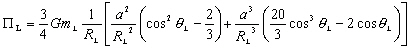 (4.14)
(4.14)
Ce potentiel ne dépend :
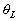 , que de la position du
point considéré à la surface de la Terre et de la
Lune par rapport au centre de la Terre ;
, que de la position du
point considéré à la surface de la Terre et de la
Lune par rapport au centre de la Terre ;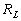 , que de la distance de
la lune par rapport au centre de la Terre.
, que de la distance de
la lune par rapport au centre de la Terre.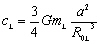 et
et 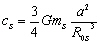
avec :
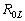 : la distance moyenne de la Terre
à la Lune ;
: la distance moyenne de la Terre
à la Lune ;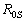 : la distance moyenne de la
Terre au Soleil.
: la distance moyenne de la
Terre au Soleil.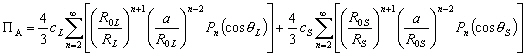 (4.15)
(4.15)
Daprès (4.14) nous pouvons écrire le potentiel luni-solaire à lordre 2 :
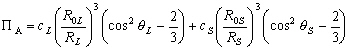
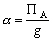 (4.16)
(4.16)
Même si la marée statique ne représente pas bien la marée réelle, elle permet dobtenir une bonne approximation de son ordre de grandeur. Ainsi, l'amplitude de la marée d'équilibre lunaire est au maximum de 54 centimètres, et la marée d'équilibre solaire est au maximum de 25 centimètres [Bessero, 1985]. La marée déquilibre luni-solaire est donc inférieure à un mètre.
Plaçons-nous dans le repère 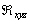 introduit en dans le paragraphe 3.3.1 dont lorigine est le centre de la
Terre. Lintersection du plan équatorial avec le plan méridien
contentant le méridien de Greenwich est laxe des x. Laxe
des y est dans le plan équatorial et perpendiculaire à
laxe des x. Laxe des z est laxe des pôles.
introduit en dans le paragraphe 3.3.1 dont lorigine est le centre de la
Terre. Lintersection du plan équatorial avec le plan méridien
contentant le méridien de Greenwich est laxe des x. Laxe
des y est dans le plan équatorial et perpendiculaire à
laxe des x. Laxe des z est laxe des pôles.
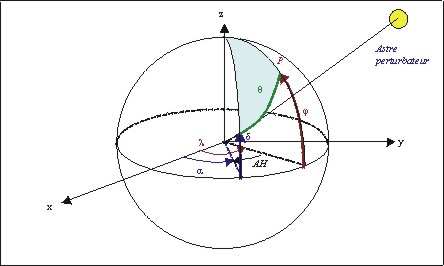
Figure 10 : Coordonnées horaires
dun astre perturbateur
Soit :
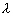 la longitude et
la longitude et 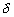 la latitude (ou déclinaison) de lastre perturbateur ;
la latitude (ou déclinaison) de lastre perturbateur ;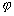 la latitude
du point P où sapplique la force génératrice ;
la latitude
du point P où sapplique la force génératrice ;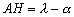 définit langle horaire
de
lastre perturbateur par rapport à la rotation de la Terre ;
définit langle horaire
de
lastre perturbateur par rapport à la rotation de la Terre ;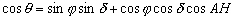 (4.17)
(4.17)
En reportant (4.17) dans (4.15) et en ne considérant quun astre, nous avons après simplifications :
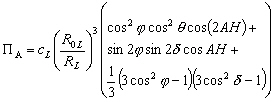 (4.18)
(4.18)
Les trois termes de la somme de (4.18) ont une dépendance différente en fonction de AH, angle horaire de lastre perturbateur considéré :
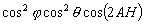 , dépendant de 2AH,
est minimum et maximum sur deux méridiens Est opposés de
90° (et leurs complémentaires respectifs à lOuest) par
révolution de lastre autour de la Terre. Sa périodicité
est donc semi-diurne. Son signe ne dépend que de celui de
, dépendant de 2AH,
est minimum et maximum sur deux méridiens Est opposés de
90° (et leurs complémentaires respectifs à lOuest) par
révolution de lastre autour de la Terre. Sa périodicité
est donc semi-diurne. Son signe ne dépend que de celui de 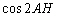 .
Donc, sur un même méridien son signe reste constant. On parle
de répartition spatiale sectorielle.
.
Donc, sur un même méridien son signe reste constant. On parle
de répartition spatiale sectorielle.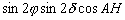 , dépendant
de AH, nest quune fois minimum et maximum sur un méridien
Est (et son complémentaire à lOuest) par révolution
de lastre autour de la Terre. Sa périodicité est donc diurne.
Son signe est dépendant de la position de lastre. On parle de répartition
spatiale téssérale.
, dépendant
de AH, nest quune fois minimum et maximum sur un méridien
Est (et son complémentaire à lOuest) par révolution
de lastre autour de la Terre. Sa périodicité est donc diurne.
Son signe est dépendant de la position de lastre. On parle de répartition
spatiale téssérale.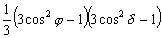 ne dépend pas
de AH. On dit que cest un terme longue période. On
parle de répartition spatiale zonale.
ne dépend pas
de AH. On dit que cest un terme longue période. On
parle de répartition spatiale zonale.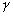 (ou équinoxe de printemps) qui est le point sur la ligne
déquinoxe (intersection de léquateur de la Terre
et de lécliptique) où le Soleil coupe le plan équatorial
le 21 mars. Ce point déquinoxe vernal a une position qui varie
très lentement au cours des siècles. La latitude est mesurée
par rapport au plan de lécliptique. La déclinaison du Soleil
est maximale au moment des solstices. Le Soleil moyen est
le Soleil fictif qui évolue le long de lécliptique à
une vitesse horaire constante.
(ou équinoxe de printemps) qui est le point sur la ligne
déquinoxe (intersection de léquateur de la Terre
et de lécliptique) où le Soleil coupe le plan équatorial
le 21 mars. Ce point déquinoxe vernal a une position qui varie
très lentement au cours des siècles. La latitude est mesurée
par rapport au plan de lécliptique. La déclinaison du Soleil
est maximale au moment des solstices. Le Soleil moyen est
le Soleil fictif qui évolue le long de lécliptique à
une vitesse horaire constante.
La distance moyenne de la Terre au Soleil
est de 149,6 millions de kilomètres. Le Soleil évolue dans
le plan de lécliptique qui fait un angle 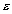 (obliquité de lécliptique) avec léquateur
terrestre variant peu au cours du temps : environ 23,45°. Lexcentricité
moyenne e du Soleil (paramètre définissant le
caractère non rigoureusement circulaire de lorbite solaire) est
de 0,017. Le point vernal bouge très légèrement le
long de lécliptique pour faire une révolution sur le plan
de lécliptique en 26000 années environ (précession
luni-solaire). Le périgée solaire (point de lorbite
le plus proche du Soleil) est à 147,1 millions de kilomètres
de la Terre. Lapogée solaire (point de lorbite le plus
éloigné du Soleil) est à 152,1 millions de kilomètres.
Le périgée solaire accomplit une révolution sidérale
en 209,4 siècles. La durée dune révolution de la
Terre est dune année tropique soit 365,24 jours.
(obliquité de lécliptique) avec léquateur
terrestre variant peu au cours du temps : environ 23,45°. Lexcentricité
moyenne e du Soleil (paramètre définissant le
caractère non rigoureusement circulaire de lorbite solaire) est
de 0,017. Le point vernal bouge très légèrement le
long de lécliptique pour faire une révolution sur le plan
de lécliptique en 26000 années environ (précession
luni-solaire). Le périgée solaire (point de lorbite
le plus proche du Soleil) est à 147,1 millions de kilomètres
de la Terre. Lapogée solaire (point de lorbite le plus
éloigné du Soleil) est à 152,1 millions de kilomètres.
Le périgée solaire accomplit une révolution sidérale
en 209,4 siècles. La durée dune révolution de la
Terre est dune année tropique soit 365,24 jours.
La Lune est à une distance moyenne
de la Terre de 384400 kilomètres. Elle évolue dans le plan
de lorbite lunaire dexcentricité moyenne égale à
0,055. Cette excentricité est moyenne car à cause des perturbations
dues au Soleil, elle varie en fait entre 0,044 et 0,067. Son inclinaison
moyenne i par rapport à lécliptique est de 5,15°
et varie entre 5° et 5,3°. Le nud ascendant lunaire 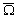 est le point dintersection de lorbite lunaire avec le plan de lécliptique
quand le mouvement de la Lune est dirigé vers le nord. Linclinaison
I
de lorbite lunaire par rapport à léquateur varie au cours
du temps en fonction de la position de
est le point dintersection de lorbite lunaire avec le plan de lécliptique
quand le mouvement de la Lune est dirigé vers le nord. Linclinaison
I
de lorbite lunaire par rapport à léquateur varie au cours
du temps en fonction de la position de 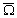 : de 18,5° quand
: de 18,5° quand 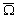 coïncide
avec
coïncide
avec 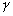 à 28,5° quand
à 28,5° quand 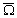 coïncide
avec léquinoxe dautomne (le point diamétralement
opposé à
coïncide
avec léquinoxe dautomne (le point diamétralement
opposé à 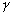 , cest-à-dire
le point sur la ligne déquinoxe où le Soleil coupe
le plan équatorial le 23 septembre). La périodicité
de passage de
, cest-à-dire
le point sur la ligne déquinoxe où le Soleil coupe
le plan équatorial le 23 septembre). La périodicité
de passage de 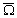 sur
sur 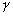 est de 18,61 années, ce qui entraîne un mouvement annuel de
est de 18,61 années, ce qui entraîne un mouvement annuel de 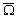 dans la direction ouest de 19,57° par an : cest la régression.
Par commodité dans létude des marées, linclinaison
de la Lune sur lécliptique et lexcentricité lunaire variant
très lentement dans le temps, des valeurs moyennes dépendant
de la date considérée suffisent aux calculs. Le périgée
lunaire est à 363296 kilomètres de la Terre. Lapogée
lunaire est à 405504 kilomètres. La durée dune révolution
sidérale de la Lune est égale en moyenne à 27,32 jours
et celle du périgée lunaire à 8,85 années tropiques.
dans la direction ouest de 19,57° par an : cest la régression.
Par commodité dans létude des marées, linclinaison
de la Lune sur lécliptique et lexcentricité lunaire variant
très lentement dans le temps, des valeurs moyennes dépendant
de la date considérée suffisent aux calculs. Le périgée
lunaire est à 363296 kilomètres de la Terre. Lapogée
lunaire est à 405504 kilomètres. La durée dune révolution
sidérale de la Lune est égale en moyenne à 27,32 jours
et celle du périgée lunaire à 8,85 années tropiques.
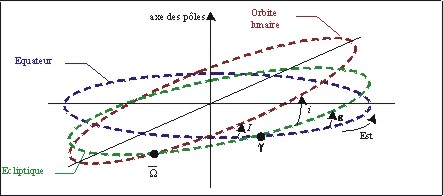
Figure 11 : Caractéristiques
des mouvements de la Terre, la Lune et le Soleil
Pendant la durée de rotation de la Terre par rapport aux étoiles fixes (jour sidéral), le Soleil sest déplacé lui aussi le long de lécliptique dans le sens inverse de la rotation terrestre. Donc le jour solaire moyen (passage du Soleil moyen au-dessus dun même méridien terrestre après une rotation autour de la Terre) est légèrement plus court (23h56min) que le jour sidéral. Au contraire, la Lune se déplace le long de son orbite dans le même sens que laxe de rotation terrestre. Le jour lunaire moyen est donc plus long que le jour sidéral soit 24h50min28s. Les pleines lunes et les nouvelles lunes ont lieu à chaque fois que la Lune repasse au même point du plan de lécliptique soit tous les 29,53 jours : cest la lunaison.
Nous avons insisté sur les nombreuses périodes des différents phénomènes résultants de la rotation des astres perturbateurs (Lune et Soleil) autour de la Terre, car elles vont se retrouver dans les périodicités des composantes de la marée. Toutes les périodicités décrites ci-dessus sont incommensurables deux à deux, cest-à-dire que les mouvements des deux astres perturbateurs nengendrent pas une force génératrice des marées périodique au sens strict. En effet, il nexiste pas de période au bout de laquelle le phénomène de marée (et donc lélévation du niveau des océans due aux marées) soit identique. Cependant, il existe une période au bout de laquelle la configuration est quasiment identique. Cest la période chaldéenne ou période de Saros qui correspond à :
| Longitude moyenne |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 3 : Valeurs des angles fondamentaux des mouvements de la Lune et du Soleil
Considérons le temps en jours juliens diminué du nombre de jours juliens écoulés au 31 décembre 1899, minuit temps universel. Dans la période julienne, la date dorigine est le 1er janvier 4713 avant J.-C. à midi (calendrier julien). La journée qui sépare le midi du 1er janvier à celui du deux janvier porte le numéro 0. Soit T le nombre de siècles juliens (soit 36525 jours solaires moyens).
Afin que tous les angles augmentent vers
lest, Doodson a défini 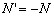 .
Avec cette convention temporelle, les 5 angles fondamentaux sont alors
[Doodson, 1921] :
.
Avec cette convention temporelle, les 5 angles fondamentaux sont alors
[Doodson, 1921] :
 (4.19)
(4.19)
Enfin, le temps moyen solaire de Greenwicht
et le temps moyen lunaire de Greenwich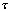 par la relation sont définis par :
par la relation sont définis par :
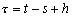 (4.20)
(4.20)
Le Tableau 4 donne les périodes des angles fondamentaux.
|
|
|
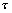 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 4 : Périodes des angles fondamentaux
Chaque onde est caractérisée par une appellation symbolique composée dune lettre pour indiquer le groupe auquel elle appartient (M, S, O, N, K, Q, s, r, t, c...) et dun indice pour indiquer sa périodicité :
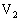 (développement
à lordre 2 de la série en polynômes de Legendre) est
alors exprimé sous la forme :
(développement
à lordre 2 de la série en polynômes de Legendre) est
alors exprimé sous la forme :
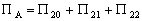 (4.21)
(4.21)
avec :
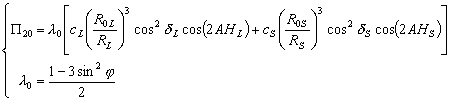 (4.22)
(4.22)
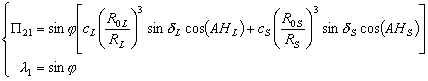 (4.23)
(4.23)
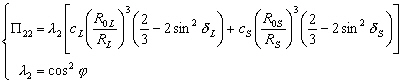 (4.24)
(4.24)
Les 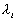 sont appelés les facteurs de latitude : ce sont eux qui déterminent
le type de la marée. Ils dépendent de
sont appelés les facteurs de latitude : ce sont eux qui déterminent
le type de la marée. Ils dépendent de 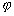 la latitude à laquelle le potentiel sexerce. Les coefficients
la latitude à laquelle le potentiel sexerce. Les coefficients 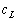 et
et 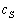 sont définis dans
le paragraphe 4.2.2.3.
sont définis dans
le paragraphe 4.2.2.3. 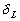 et
et 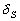 sont les déclinaisons respectives de la Lune et du Soleil, et
sont les déclinaisons respectives de la Lune et du Soleil, et 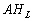 et
et 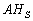 , leurs angles horaires respectifs.
, leurs angles horaires respectifs.
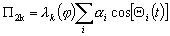 (4.25)
(4.25)
avec :
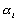 les coefficients positifs du développement
harmonique ;
les coefficients positifs du développement
harmonique ;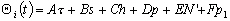 les arguments astronomiques
(ou arguments de Doodson) au méridien de Greenwich avec A,
B,
C,
D, E et F des nombres entiers et t lheure
civile du lieu considéré.
les arguments astronomiques
(ou arguments de Doodson) au méridien de Greenwich avec A,
B,
C,
D, E et F des nombres entiers et t lheure
civile du lieu considéré.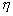 est
:
est
:
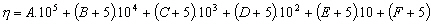 (4.26)
(4.26)
Les composantes ayant le même A constituent une espèce. Les composantes qui ont le même A et le même B constituent un groupe. Enfin, celles qui ont le même A, le même B et le même C constituent un sous-groupe.
Nous reportons dans le Tableau 5 les principales composantes et leurs caractéristiques. Tous les coefficients ont été recalculés par nos soins. Lorigine de londe est Lunaire (L) ou Solaire (S). Ces calculs nous ont permis dune part de vérifier les calculs de Doodson et dautre part ajouter les fréquences en radians par secondes des différentes ondes du spectre de marée. Ce tableau corrobore et complète les travaux de Doodson.
De ce Tableau 5, nous pouvons tirer plusieurs
remarques. Bien que le développement de Doodson comporte plus de
400 composantes, celles qui sont sélectionnées ci-dessus
représentent la plus grande partie de celles du potentiel générateur.
Grâce à la période calculée des composantes,
nous retrouvons les trois grandes classifications (espèces) des
ondes de marée : les longues périodes (périodes supérieures
au jour), les diurnes (périodes de lordre de la journée)
et les semi-diurnes (périodes de lordre de la demi-journée).
Enfin, ce qui caractérise principalement les trois différentes
espèces, cest 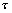 , le temps
solaire moyen multiplié par un coefficient égal à
0 pour les longues périodes, 1 pour les diurnes et 2 pour les semi-diurnes.
, le temps
solaire moyen multiplié par un coefficient égal à
0 pour les longues périodes, 1 pour les diurnes et 2 pour les semi-diurnes.
|
|
|
Doodson |
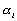 |
(°/h) |
(rad/s) |
(jours) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
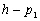 |
|
|
|
|
|
|
|
|
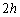 |
|
|
|
|
|
|
|
|
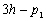 |
|
|
|
|
|
|
|
|
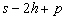 |
|
|
|
|
|
|
|
|
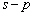 |
|
|
|
|
|
|
|
|
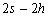 |
|
|
|
|
|
|
|
|
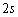 |
|
|
|
|
|
|
|
|
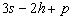 |
|
|
|
|
|
|
|
|
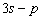 |
|
|
|
|
|
|
|
|
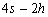 |
|
|
|
|
|
|
|
|
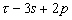 |
|
|
|
|
|
| s1 |
|
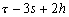 |
|
|
|
|
|
|
|
|
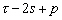 |
|
|
|
|
|
| r1 |
|
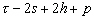 |
|
|
|
|
|
|
|
|
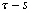 |
|
|
|
|
|
| t1 |
|
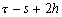 |
|
|
|
|
|
|
|
|
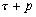 |
|
|
|
|
|
|
|
|
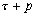 |
|
|
|
|
|
| c1 |
|
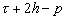 |
|
|
|
|
|
| p1 |
|
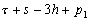 |
|
|
|
|
|
|
|
|
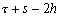 |
|
|
|
|
|
|
|
|
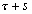 |
|
|
|
|
|
|
|
|
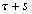 |
|
|
|
|
|
| y1 |
|
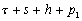 |
|
|
|
|
|
| j1 |
|
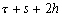 |
|
|
|
|
|
| q1 |
|
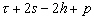 |
|
|
|
|
|
|
|
|
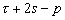 |
|
|
|
|
|
|
|
|
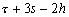 |
|
|
|
|
|
|
|
|
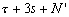 |
|
|
|
|
|
| n1 |
|
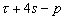 |
|
|
|
|
|
| e2 |
|
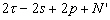 |
|
|
|
|
|
|
|
|
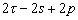 |
|
|
|
|
|
| m2 |
|
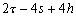 |
|
|
|
|
|
|
|
|
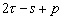 |
|
|
|
|
|
| n2 |
|
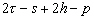 |
|
|
|
|
|
|
|
|
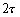 |
|
|
|
|
|
| l2 |
|
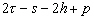 |
|
|
|
|
|
|
|
|
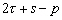 |
|
|
|
|
|
|
|
|
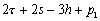 |
|
|
|
|
|
|
|
|
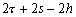 |
|
|
|
|
|
|
|
|
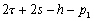 |
|
|
|
|
|
|
|
|
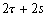 |
|
|
|
|
|
|
|
|
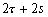 |
|
|
|
|
|
Tableau 5 : Principales composantes extraites du développement de Doodson (calculs de lauteur)
Le nom donné par Darwin à chacune des composantes de la marée (M2, K1 ) caractérise lorigine de la force génératrice élémentaire. Déterminons lorigine des principales ondes de marée suivant lamplitude donnée par le coefficient harmonique du développement de Doodson (cf. Tableau 5). La composante la plus importante est M2(en anglais : M=Moon, 2=semi-diurne). Cest la composante lunaire principale due à un astre fictif de la taille de la Lune évoluant suivant une orbite circulaire dans le plan de léquateur terrestre. Sa période est de 0,5175 jours soit 12h25min, ce qui correspond approximativement à la période séparant deux basses mers et deux pleines mers le long des côtes atlantiques européennes (la moitié du jour lunaire moyen). Elle est encadrée par plusieurs composantes à variations elliptiques de sa période dont les deux plus importantes sont L2 lelliptique lunaire mineure de M2 et N2 lelliptique lunaire majeure de M2 (la lettre M est entre L et N dans lalphabet). N2 est induite par les variations de la distance entre la Terre et la Lune. Léquivalent de M2 pour la lune est S2 pour le Soleil (en anglais : S=Sun, 2=semi-diurne) dont la période est exactement 0,5 jours soit 12h00min ce qui correspond à une demi-journée de jour sidéral. S2 est elle aussi encadrée de plusieurs composantes à variations elliptiques de sa période. Les deux plus importantes sont R2 lelliptique solaire mineure de S2 et T2 lelliptique solaire majeure de S2 (R et T encadrent S). Enfin il existe K2L et K2S deux composantes qui, ayant le même nombre de Doodson et la même période mais dont lune à pour origine la Lune et lautre le Soleil, sont dénommées de manière identique. Cest pourquoi K2 est nommée déclinationnelle luni-solaire semi-diurne. Elle est liée à la variation des déclinaisons de la Lune et du Soleil.
Les ondes de lespèce diurne sont dues à la déclinaison de la Lune et su Soleil. Elles engendrent des inégalités diurnes de la force génératrice des marées. La composante principale est K1. Tout comme K2, elle se compose dune partie lunaire, K1L et dune partie solaire K1S. K1 est nommée déclinationnelle luni-solaire diurne. Sa période est de 0,9973 jours soit 23h56min11s. O1 est la composante lunaire diurne principale et est induite par les variations de la déclinaison de la Lune. P1 est la composante solaire diurne principale et est générée par les variations de déclinaison du Soleil. K1 et O1sont encadrées de plusieurs composantes qui correspondent à des variations elliptiques par rapport à leurs périodes. Ainsi, Q1 est la composante elliptique majeure de O1.
Enfin, lespèce des longues périodes est plus particulière. M0 et S0correspondent aux termes permanents de la marée. M0 est londe lunaire permanente et S0 est londe solaire permanente. En considérant une Terre entièrement recouverte dune fine pellicule deau correspondant aux océans, léquilibre statique est tout le temps vérifié pour les ondes longues périodes. Les continents ont donc très peu dinfluence sur cette espèce donde. Dans le développement harmonique de Doodson, la Terre est supposée rigide, ce qui nest pas le cas. En effet, elle présente une certaine élasticité, qui fait que la force génératrice des marées sapplique, elle aussi, aux continents et aux terres submergées. La marée calculée nest donc pas la marée réelle, car le plancher océanique se soulève et sabaisse lui aussi. Il faut donc tenir compte de ce phénomène pour obtenir la marée réelle. Les termes permanents de la marée sont représentatifs de ce phénomène. En général, leurs effets sont pris en compte dans le phénomène des marées terrestres qui sont soustraites aux marées calculées pour accéder à la marée réelle (cf. Chapitre 6). Sa est londe solaire annuelle (en anglais : S=Sun, a=annual) due aux variations de la longitude moyenne du Soleil par rapport à son périgée. Sa période est légèrement supérieure à lannée tropique soit 365,26 jours. De même pour la Lune, il existe Mm qui est londe lunaire moyenne mensuelle (en anglais : M=Moon, m=monthly), de période 27,55 jours soit un peu plus que la durée dune révolution sidérale moyenne de la Lune. Enfin, les variations des déclinaisons du Soleil et de la Lune engendrent respectivement Ssa (en anglais : S=Sun, sa=semi-annual) londe déclinationnelle solaire semi-annuelle et Mf (en anglais : M=Moon, f=fortnigthly) londe déclinationnelle lunaire semi-mensuelle.
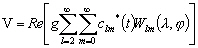 (4.27)
(4.27)
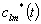 étant le conjugué complexe qui correspond à la marée
déquilibre à Greenwich, de degré l et dordre
m.
Les parties réelles et imaginaires de
étant le conjugué complexe qui correspond à la marée
déquilibre à Greenwich, de degré l et dordre
m.
Les parties réelles et imaginaires de 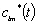 comprennent les paramètres nodaux [Munk and Cartwright, 1966].
Les
comprennent les paramètres nodaux [Munk and Cartwright, 1966].
Les 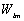 sont les harmoniques sphériques
complexes qui dépendent uniquement du lieu considéré
:
sont les harmoniques sphériques
complexes qui dépendent uniquement du lieu considéré
:
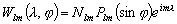 (4.28)
(4.28)
avec :
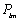 le polynôme de Legendre ;
le polynôme de Legendre ;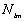 des facteurs de normalisation.
des facteurs de normalisation.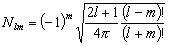 (4.29)
(4.29)
Cartwright et Tayler ont directement calculé les éphémérides de la Lune et du Soleil et ils ont pris en compte la très légère variation de langle de lécliptique avec léquateur terrestre. Ce qui entraîne que leurs coefficients harmoniques du potentiel générateur, contrairement à ceux de Doodson, varient très légèrement dans le temps. Le développement du potentiel par Doodson est analytique tandis que celui de Cartwright et Tayler en extrait les différents termes du potentiel en faisant une FFT (Fast Fourier Transform) déphémérides. Cependant, les résultats sont très comparables. Les écarts entre les coefficients harmoniques de Doodson et ceux de Cartwright et Tayler nexcèdent pas 0,1%.
Cest pourquoi, dans la suite de notre étude, nous utiliserons le développement du potentiel générateur de Doodson pour tous nos calculs.