Chapitre 5 Les équations générales
de la marée
5.1 Présentation du chapitre
Les développements du potentiel générateur
de la marée du chapitre précédent nous permettent
d’envisager une résolution de la marée par des méthodes
harmoniques. L’introduction des équations de marées en plein
océan et en petits fonds va nous permettre de modéliser la
marée. En particulier la linéarisation du coefficient de
frottement autorise la résolution de ces équations tout à
la fois en zones pélagiques et en zones littorales. Cette linéarisation
fait apparaître d’autres ondes non harmoniques présentes dans
le spectre de marée qui seront caractérisées.
5.2 Réponse de l’océan
à l’excitation du potentiel générateur
5.2.1 Equations des ondes longues
5.2.1.1 Equations de Navier-Stokes
La mécanique des fluides nous donne
les équations du mouvement d’un fluide de viscosité constante
en milieu tournant. Ce sont les équations de Navier-Stokes
[Gill, 1982] :
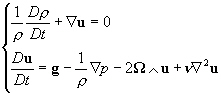 (5.30)
(5.30)
avec :
-
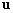 : la vitesse d’une particule d’eau
;
: la vitesse d’une particule d’eau
;
-
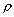 : la masse volumique de l’eau ;
: la masse volumique de l’eau ;
-
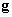 : la pesanteur supposée constante
;
: la pesanteur supposée constante
;
-
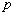 : la pression de l’eau ;
: la pression de l’eau ;
-
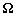 : le vecteur de rotation de la Terre
supposé constant ;
: le vecteur de rotation de la Terre
supposé constant ;
La première équation de (5.30)
est l’équation de continuité (ou équation
de conservation de la masse) et la deuxième est l’équation
de conservation de la quantité de mouvement.
Par définition la dérivé
particulaire est :
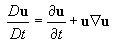
5.2.1.2 Hypothèse des ondes
longues
Dans le cadre de l’étude des marées
océaniques la résolution des équations de la marée
est complexe. Il faut les simplifier pour obtenir les équations
de Laplace [Pekeris and Accad, 1969]. Ainsi, plusieurs approximations
(légitimes comme nous allons le voir) doivent être faites.
C’est pourquoi, nous assimilerons l’eau à un fluide incompressible.
Nous négligerons les effets de la turbulence et donc, nous ne tiendrons
pas compte des effets de viscosité. Dans ce cas, les équations
de Navier-Stokes définies en (5.30) se simplifient et deviennent
dans le repère terrestre 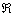 défini dans le paragraphe 3.3.1 :
défini dans le paragraphe 3.3.1 :
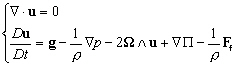 (5.31)
(5.31)
avec :
-
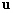 : la vitesse d’une particule d’eau
;
: la vitesse d’une particule d’eau
;
-
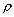 : la masse volumique constante de
l’eau puisqu’elle est supposée incompressible ;
: la masse volumique constante de
l’eau puisqu’elle est supposée incompressible ;
-
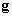 : la pesanteur supposée constante
;
: la pesanteur supposée constante
;
-
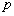 : la pression de l’eau ;
: la pression de l’eau ;
-
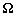 : le vecteur de rotation de la Terre
supposé constant ;
: le vecteur de rotation de la Terre
supposé constant ;
-
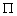 : le potentiel astronomique générateur
des marées ;
: le potentiel astronomique générateur
des marées ;
-
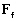 : une force de frottement sur le
plancher océanique.
: une force de frottement sur le
plancher océanique.
Pour étudier les marées, deux
hypothèses supplémentaires sont à considérer
:
-
la composante verticale de la vitesse est négligeable devant les
composantes horizontales ;
-
le fluide est barotrope, c’est-à-dire que sur une même verticale,
toutes les particules d’eau se déplacent à la même
vitesse (même module, même direction, même sens).
Ces deux approximations constituent l’hypothèse
des ondes longues. La première hypothèse est justifiée
par les observations. L’amplitude de la marée est de l’ordre du
mètre, alors que pour les ondes semi-diurnes la période est
d’une demi-journée. C’est-à-dire que les ondes de marées
parcourent le tour de la Terre (environ 40000 km) en 12h environ et s’élèvent
et s’abaissent d’un mètre environ pendant cette même période.
Les vitesses verticales sont donc négligeables. La seconde hypothèse
se justifie par le fait que les océans sont une couche de fluide
mince à la surface de la Terre. En effet, la profondeur moyenne
des océans est de l’ordre de 4 kilomètres alors que leurs
dimensions horizontales sont de l’ordre du millier de kilomètres.
Le déplacement des masses d’eau peut donc être considéré
comme uniforme sur toute la colonne d’eau.
En outre à (5.31), il faut ajouter
des conditions aux limites, en surface (la pression de l’eau est égale
à la pression atmosphérique) et au fond (vitesse normale
au plancher océanique donc nulle au fond).
Avec l’hypothèse de la vitesse horizontale
nulle, on montre que :
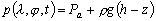 (5.32)
(5.32)
avec :
-
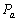 : la pression atmosphérique
à la surface des océans ;
: la pression atmosphérique
à la surface des océans ;
-
h : la hauteur instantanée de la colonne d’eau du fond à
la surface en un point de coordonnées
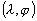 ;
;
-
t : le temps donné.
Nous avons :
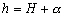 (5.33)
(5.33)
avec :
-
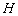 : la profondeur constante d’un océan
au point considéré ;
: la profondeur constante d’un océan
au point considéré ;
-
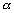 : l’élévation de surface
due à la marée.
: l’élévation de surface
due à la marée.
Avec toutes ces hypothèses justifiées
dans le cadre de l’étude des marées océaniques qui
sont des ondes longues, (5.31) se simplifie en :
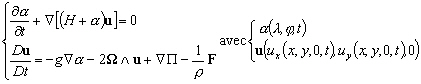 (5.34)
(5.34)
5.2.2 Equations linéarisées
de la marée
Loin des côtes, les courants de marée
sont très faibles, tout comme leurs dérivées spatiales,
donc :
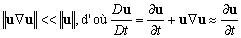 (5.35)
(5.35)
De plus, comme nous l’avons vu, 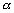 reste petit devant H au large donc :
reste petit devant H au large donc :
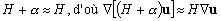 (5.36)
(5.36)
Enfin, au large, les forces de frottement
sont négligeables par rapport aux autres forces en jeu. En effet,
la couche turbulente qui se développe par frottement sur le fond
est de dimension négligeable par rapport à la colonne d’eau
considérée et mise en mouvement par la force génératrice
des marées. Donc nous obtenons grâce à (5.35) et (5.36)
une linéarisation de (5.34). Ce sont les équations linéarisées
de la marée :
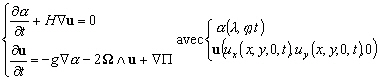 (5.37)
(5.37)
5.2.3 Equations des marées
littorales
En zones littorales (petits fonds, zones côtières,
mers littorales, plateaux océaniques…) les hypothèses faites
pour obtenir les équations linéarisées de la marée
ne sont plus applicables. D’une part, nous ne pouvons négliger le
terme de frottement sur le plancher océanique car la couche limite
turbulente développée sur le fond par la colonne d’eau, mise
en mouvement par la force génératrice des marées,
est de l’ordre de la dimension de cette colonne. D’autre part, nous ne
pouvons plus négliger les termes non linéaires des vitesses
car les gradients topographiques en petits fonds modifient rapidement la
hauteur de la colonne d’eau en mouvement.
Les hypothèses classiques qui caractérisent
les marées littorales [Hyacinthe and Kravtchenko, 1967] sont
adaptées à notre cas par Le Provost [1973] :
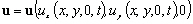
-
: la vitesse verticale est négligeable par rapport aux vitesses
horizontales et les composantes de la vitesse ne dépendent pas de
la verticale ;
-
la viscosité du fluide est négligeable ;
-
le frottement de fond équivaut à une force.
Ainsi, cette force de frottement 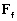 est
donnée par :
est
donnée par :
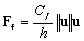 (5.38)
(5.38)
avec :
-
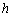 : la profondeur d’eau instantanée
(
: la profondeur d’eau instantanée
(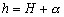 )
)
-
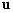 : la vitesse barotrope horizontale
: la vitesse barotrope horizontale
-
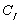 : le coefficient de frottement sans
dimension de type Chézy
: le coefficient de frottement sans
dimension de type Chézy
Le coefficient de frottement est déterminé
empiriquement. Nous donnons dans les chapitres suivants des ordres de grandeurs
et des valeurs de ce coefficient. C’est un terme quadratique.
Avec (5.34) et (5.38), nous obtenons les
équations des marées littorales :
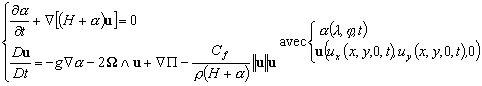 (5.39)
(5.39)
5.3 Influence du coefficient de frottement
5.3.1 Expression du niveau de la surface
océanique due au potentiel
Comme nous l’avons vu dans le Chapitre 4,
le potentiel générateur des marées peut se décomposer
en une somme de fonctions sinusoïdales élémentaires.
L’expression des équations linéarisées de la marée
amène donc à chercher la dénivellation du niveau des
océans créée par la force génératrice
des marées, dont dérive le potentiel, sous la forme d’une
somme de fonctions sinusoïdales élémentaires :
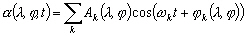 (5.40)
(5.40)
où :
-
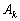 est l’amplitude de la composante
k de la dénivellation due à la marée ;
est l’amplitude de la composante
k de la dénivellation due à la marée ;
-
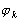 est la phase de la composante k
de la dénivellation due à la marée ;
est la phase de la composante k
de la dénivellation due à la marée ;
-
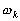 est la fréquence de la composante
k : elle est donnée par le développement de Doodson.
est la fréquence de la composante
k : elle est donnée par le développement de Doodson.
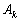 et
et 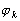 ne dépendent que de la position du point considéré
à la surface des océans (latitude et longitude).
ne dépendent que de la position du point considéré
à la surface des océans (latitude et longitude).
En fait une expression plus complète
de la dénivellation de la surface libre est donnée par Doodson
:
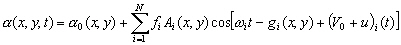 (5.41)
(5.41)
avec :
-
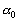 le niveau moyen ;
le niveau moyen ;
-
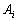 l’amplitude de l’onde i ;
l’amplitude de l’onde i ;
-
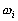 la fréquence de l’onde i
;
la fréquence de l’onde i
;
-
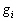 le déphasage de l’onde i
par rapport au passage de l’astre perturbateur au méridien de Greenwich
;
le déphasage de l’onde i
par rapport au passage de l’astre perturbateur au méridien de Greenwich
;
-
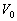 la phase de l’astre perturbateur
à l’origine des temps ;
la phase de l’astre perturbateur
à l’origine des temps ;
-
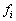 le coefficient de correction nodale
d’amplitude pour l’onde i.
le coefficient de correction nodale
d’amplitude pour l’onde i.
-
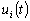 le coefficient de correction nodale
de phase pour l’onde i ;
le coefficient de correction nodale
de phase pour l’onde i ;
Les coefficients de correction nodale représentent
les très faibles variations des nœuds des astres perturbateurs sur
l’écliptique. Des valeurs de ces coefficients sont données
par Schureman [1958].
5.3.2 Expression des vitesses dues
au potentiel
Comme les vitesses de marées dérivent
directement de la dénivellation, nous pouvons aussi rechercher ces
vitesses sous la décomposition similaire de somme de fonctions sinusoïdales
élémentaires :
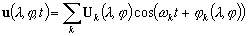 (5.42)
(5.42)
5.3.3 Introduction du coefficient
de frottement
L’introduction d’un terme de frottement dans
les équations de marées permet une meilleure modélisation
du phénomène en zones côtières. Jusqu’à
présent, nous n’avons considéré que les ondes de marées
générées par le potentiel astronomique. Ces ondes
sont dites ondes astronomiques. Cependant, nous allons voir dans
la suite que d’autres ondes s’ajoutent au spectre de marée. En effet,
du fait de la complexité non-linéaire de la propagation des
ondes de marées en petits fonds, des ondes apparaissent. Nous les
retrouvons dans la décomposition du terme de frottement de fond.
Ces ondes non linéaires apparaissent avec des fréquences
supérieures à celles des ondes astronomiques.
Les équations de la marée
posent un problème de taille : le coefficient de frottement est
un terme quadratique de la vitesse, alors que le reste des équations
est linéaire. Linéariser le terme de frottement permettrait
donc de linéariser les équations de la marée et ainsi
de les résoudre. Dans son travail de thèse, Le Provost
[1973] a décomposé le terme quadratique de frottement d’une
marée multipériodique dans un domaine bidimensionnel, à
la condition qu’une composante du spectre de la marée étudiée
soit dominante. Par définition une onde de marée est dite
dominante, si l’amplitude de sa vitesse est toujours strictement positive
et si l’amplitude maximale de sa vitesse dépasse strictement la
vitesse résultante créée par l’ensemble des autres
composantes. Cette dernière hypothèse est largement vérifiée
de par le monde, grâce aux nombreux spectres de marées déduits
de l’analyse des signaux relevés par les marégraphes. En
général, l’onde dominante est M2 voire
K1.
C’est donc une constatation expérimentale.
Le Provost [1973]
a cherché les développements limités généralisés
de Fourier des deux composantes du coefficient de frottement et en a donné
l’expression grâce à une hypothèse, vérifiée
expérimentalement dans la Manche, d’existence d’une onde dominante.
5.3.4 Décomposition du coefficient
de frottement
Les travaux de Le Provost [1973] finalisés
avec ceux de Le Provost et al. [1981] donnent l’expression linéarisée
du coefficient de frottement. Cette formulation est rappelée dans
le Chapitre 6 quand nous introduisons les équations spécifiquement
utilisées dans le modèle hydrodynamique.
5.4 Ondes de marées non astronomiques
5.4.1 Ondes non linéaires
Grâce à la linéarisation
du coefficient de frottement, nous pouvons donc introduire les expressions
sinusoïdales (5.40) de la dénivellation dans (5.39). Du fait
du terme quadratique 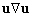 , des termes
en
, des termes
en 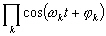 apparaissent.
apparaissent.
Par les formules de linéarisations
trigonométriques, nous pouvons simplifier ces produits de fonctions
sinusoïdales en :
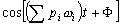
avec :
-
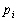 des entiers négatifs, positifs
ou nuls ;
des entiers négatifs, positifs
ou nuls ;
-
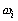 des fréquences des composantes
astronomiques de marées ;
des fréquences des composantes
astronomiques de marées ;
-
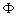 une phase associée.
une phase associée.
Ainsi, des termes provenant de la non-linéarité
du coefficient de frottement sont déduits des équations de
la marée. Ces termes ont des fréquences particulières
qui sont des combinaisons linéaires des fréquences des composantes
astronomiques, chacune pondérée par un entier. Ces nouvelles
ondes qui apparaissent en petits fonds sont des ondes d’interactions
de fréquences égales à la combinaison linéaire
de deux, trois (ou plus) fréquences des termes du potentiel astronomique.
En effet elles sont bien la conséquence de l’interaction de plusieurs
ondes astronomiques.
Parmi ces ondes, nous distinguerons :
-
les ondes composées qui sont dues à l’interaction
de plusieurs ondes astronomiques différentes ;
-
les ondes supérieures qui sont dues à l’interaction
d’une onde avec elle-même.
Dans la décomposition du spectre de
marée, les ondes composées proviennent en très grande
majorité des ondes M2, S2, K2,
N2,
K1,
et O1. Les deux principales ondes qui génèrent
des ondes supérieures sont M2 et S2.
Ces ondes sont dénommées
en fonction des ondes astronomiques dont elles sont issues. Par exemple
:
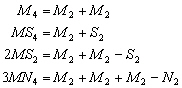
Elles sont plus ou moins importantes en
petits fonds car elles sont largement dépendantes de la géométrie
du milieu où se propagent les ondes astronomiques de marées
. En effet, étant formées par le frottement de la colonne
d’eau considérée sur le fond océanique, elles sont
générées par l’amplification de certaines ondes par
résonance ou réflexion sur la rugosité du fond et
des côtes. Les ondes non linéaires les plus importantes sont
données dans le Tableau 6 [Bessero, 1985].
Nom de
Darwin
|
Nombre de
Doodson
|
Fréquence
(°/h)
|
Période
(jours)
|
Espèce
|
|
2SM2
|
291.555
|
31,0158958
|
0,48362298
|
semi-diurne
|
|
2MS2
|
237.555
|
27,9682084
|
0,53632323
|
semi-diurne
|
|
M4
|
455.555
|
57,9682084
|
0,25876253
|
quart-diurne
|
|
MS4
|
473.555
|
58,9841042
|
0,2543058
|
quart-diurne
|
|
M6
|
655.555
|
86,9523127
|
0,17250835
|
sixième-diurne
|
|
2MS6
|
673.555
|
87,9682084
|
0,17051615
|
sixième-diurne
|
|
M8
|
863.655
|
115,9364169
|
0,12938126
|
sixième-diurne
|
|
3MS8
|
873.555
|
116,9523127
|
0,1282574
|
huitième-diurne
|
Tableau 6 : Principales composantes non linéaires
Il faut noter que certaines ondes non-linéaires
ont exactement la même fréquence que certaines ondes astronomiques.
Ainsi en est-il de 2MS2 et de 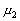 (fréquence de 27,9682084°/h) ainsi que de 2MN2
et L2 (fréquence de 29,5377626°/h). Au cours
de l’analyse harmonique d’un signal de marée mesuré, il est
donc impossible de distinguer la partie astronomique et la partie non-linéaire
de ces ondes de même fréquence.
(fréquence de 27,9682084°/h) ainsi que de 2MN2
et L2 (fréquence de 29,5377626°/h). Au cours
de l’analyse harmonique d’un signal de marée mesuré, il est
donc impossible de distinguer la partie astronomique et la partie non-linéaire
de ces ondes de même fréquence.
5.4.2 Ondes météorologiques
Nous avons vu que nous pouvons trouver dans
le spectre de marée des ondes d’origine non linéaire. Mais
ce ne sont pas les seules ondes d’origine non astronomique. En effet d’autres
phénomènes qui, s’ils sont périodiques, peuvent générer
des ondes périodiques qui s’inséreront dans le spectre. Ainsi,
le vent établi ou le réchauffement de l’eau par Soleil peut
générer des ondes périodiques. Les trois seules ondes
d’origine météorologique prises en compte dans l’étude
des marées sont S1, Sa, et Ssa.
Elles font aussi toutes les trois parties du potentiel astronomique mais
ont des coefficients très faibles. Leurs origines sont donc principalement
météorologiques :
-
Sa est due aux variations saisonnières des vents
d’alizés et des moussons (d’où cette périodicité
annuelle) ;
-
Ssa est due à l’effet stérique c’est-à-dire
l’élévation des eaux de surface dues au Soleil qui, en été,
réchauffe plus l’hémisphère Nord alors qu’en hiver,
il réchauffe plus les eaux de l’hémisphère sud (d’où
cette périodicité semestrielle) ;
-
S1 est due à des phénomènes d’alternance
entre les brises de mers et les brises de terres, d’où son origine
solaire.
Nom de
Darwin
|
Nombre de
Doodson
|
Fréquence
(°/h)
|
Période
(jours)
|
Espèce
|
|
Sa
|
056.555
|
0,0410667
|
365,2594
|
longue période
|
|
Ssa
|
057.555
|
0,0821373
|
182,6211
|
longue période
|
|
S1
|
164.555
|
15,000000
|
1,0000
|
diurne
|
Tableau 7 : Principales composantes météorologiques
Back |
Next
Title: Thèse de Fabien Lefèvre
Issue: Version 1.0
Date: 29/09/2000
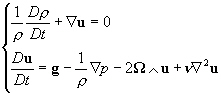 (5.30)
(5.30)
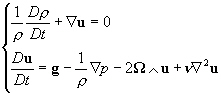 (5.30)
(5.30)
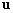 : la vitesse d’une particule d’eau
;
: la vitesse d’une particule d’eau
;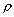 : la masse volumique de l’eau ;
: la masse volumique de l’eau ;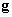 : la pesanteur supposée constante
;
: la pesanteur supposée constante
;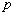 : la pression de l’eau ;
: la pression de l’eau ;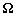 : le vecteur de rotation de la Terre
supposé constant ;
: le vecteur de rotation de la Terre
supposé constant ;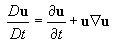
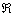 défini dans le paragraphe 3.3.1 :
défini dans le paragraphe 3.3.1 :
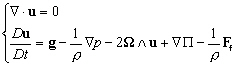 (5.31)
(5.31)
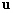 : la vitesse d’une particule d’eau
;
: la vitesse d’une particule d’eau
;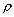 : la masse volumique constante de
l’eau puisqu’elle est supposée incompressible ;
: la masse volumique constante de
l’eau puisqu’elle est supposée incompressible ;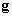 : la pesanteur supposée constante
;
: la pesanteur supposée constante
;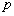 : la pression de l’eau ;
: la pression de l’eau ;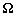 : le vecteur de rotation de la Terre
supposé constant ;
: le vecteur de rotation de la Terre
supposé constant ;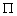 : le potentiel astronomique générateur
des marées ;
: le potentiel astronomique générateur
des marées ;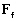 : une force de frottement sur le
plancher océanique.
: une force de frottement sur le
plancher océanique.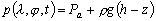 (5.32)
(5.32)
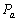 : la pression atmosphérique
à la surface des océans ;
: la pression atmosphérique
à la surface des océans ;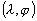 ;
;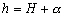 (5.33)
(5.33)
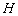 : la profondeur constante d’un océan
au point considéré ;
: la profondeur constante d’un océan
au point considéré ;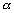 : l’élévation de surface
due à la marée.
: l’élévation de surface
due à la marée.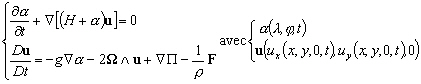 (5.34)
(5.34)
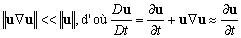 (5.35)
(5.35)
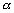 reste petit devant H au large donc :
reste petit devant H au large donc :
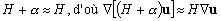 (5.36)
(5.36)
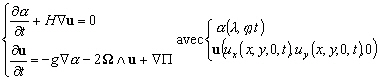 (5.37)
(5.37)
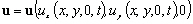
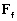 est
donnée par :
est
donnée par :
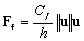 (5.38)
(5.38)
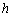 : la profondeur d’eau instantanée
(
: la profondeur d’eau instantanée
(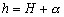 )
)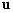 : la vitesse barotrope horizontale
: la vitesse barotrope horizontale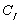 : le coefficient de frottement sans
dimension de type Chézy
: le coefficient de frottement sans
dimension de type Chézy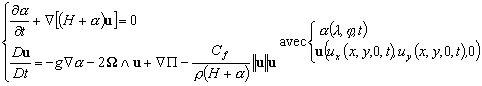 (5.39)
(5.39)
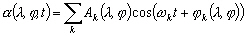 (5.40)
(5.40)
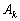 est l’amplitude de la composante
k de la dénivellation due à la marée ;
est l’amplitude de la composante
k de la dénivellation due à la marée ;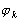 est la phase de la composante k
de la dénivellation due à la marée ;
est la phase de la composante k
de la dénivellation due à la marée ;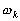 est la fréquence de la composante
k : elle est donnée par le développement de Doodson.
est la fréquence de la composante
k : elle est donnée par le développement de Doodson.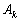 et
et 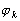 ne dépendent que de la position du point considéré
à la surface des océans (latitude et longitude).
ne dépendent que de la position du point considéré
à la surface des océans (latitude et longitude).
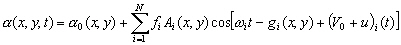 (5.41)
(5.41)
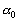 le niveau moyen ;
le niveau moyen ;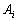 l’amplitude de l’onde i ;
l’amplitude de l’onde i ;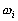 la fréquence de l’onde i
;
la fréquence de l’onde i
;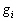 le déphasage de l’onde i
par rapport au passage de l’astre perturbateur au méridien de Greenwich
;
le déphasage de l’onde i
par rapport au passage de l’astre perturbateur au méridien de Greenwich
;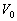 la phase de l’astre perturbateur
à l’origine des temps ;
la phase de l’astre perturbateur
à l’origine des temps ;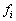 le coefficient de correction nodale
d’amplitude pour l’onde i.
le coefficient de correction nodale
d’amplitude pour l’onde i.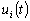 le coefficient de correction nodale
de phase pour l’onde i ;
le coefficient de correction nodale
de phase pour l’onde i ;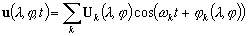 (5.42)
(5.42)
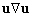 , des termes
en
, des termes
en 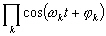 apparaissent.
apparaissent.
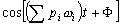
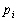 des entiers négatifs, positifs
ou nuls ;
des entiers négatifs, positifs
ou nuls ;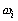 des fréquences des composantes
astronomiques de marées ;
des fréquences des composantes
astronomiques de marées ;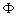 une phase associée.
une phase associée.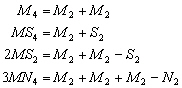
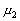 (fréquence de 27,9682084°/h) ainsi que de 2MN2
et L2 (fréquence de 29,5377626°/h). Au cours
de l’analyse harmonique d’un signal de marée mesuré, il est
donc impossible de distinguer la partie astronomique et la partie non-linéaire
de ces ondes de même fréquence.
(fréquence de 27,9682084°/h) ainsi que de 2MN2
et L2 (fréquence de 29,5377626°/h). Au cours
de l’analyse harmonique d’un signal de marée mesuré, il est
donc impossible de distinguer la partie astronomique et la partie non-linéaire
de ces ondes de même fréquence.