Chapitre 6 Le modèle hydrodynamique éléments
finis de marées
6.1 Présentation du chapitre
Dans les chapitres précédents,
nous avions simplifié la réponse de l’océan à
l’excitation du potentiel astronomique en considérant le plancher
océanique indéformable et en ne tenant pas compte des effets
internes qu’induisent les marées sur les masses d’eau qu’elles mettent
en mouvement. Nous allons maintenant tenir compte de tous ces effets supplémentaires
afin de corriger le potentiel générateur astronomique pour
obtenir le potentiel dit ‘potentiel de marée global’. Puis nous
nous intéresserons à la formulation hydrodynamique des équations
de marées afin de pouvoir les résoudre sur un maillage éléments
finis. Nous donnerons alors un aperçu de la modélisation
de la marée par notre code de calcul CEFMO (Code Eléments
Finis pour la Marée Océanique).
6.2 La marée dans le modèle
6.2.1 Définitions
Dans le cas de l’étude des marées
océaniques, il faut que nous nous fixions un référentiel.
En effet, les variations de hauteur d’eau qu’engendrent le potentiel générateur,
doivent être données en fonction d’une origine. C’est pourquoi,
il faut tenir compte de toutes les corrections à apporter au potentiel
générateur astronomique. Ces corrections sont formulées
par la suite sous forme de potentiels qui doivent être ajoutés
ou retranchés au potentiel générateur astronomique
pour obtenir le potentiel de marées qui est à l’origine des
dénivellations constatées sur l’ensemble des océans.
6.2.2 Marées terrestres astronomiques
Jusqu’à présent la Terre était
considérée comme indéformable, ce qui n’est pas le
cas en réalité. La force génératrice s’applique
aussi sur les parties terrestres de notre globe. La réponse de la
Terre à cette excitation du potentiel est statique et élastique,
comme si la Terre était une boule d’acier. Aucun courant de fluide
ne peut avoir lieu dans la partie solide. Donc, dans le cas de la Terre,
la théorie statique des marées développées
par Newton peut s’appliquer. En effet, les mouvements des particules de
la Terre ne pouvant qu’être très petits sous l’influence de
la force génératrice des marées (la matière
considérée est solide et non plus liquide), l’équilibre
est quasiment toujours atteint. Ce phénomène entraîne
donc une élévation des fonds marins. Love [1911] a
estimé cette élévation en fonction du potentiel générateur
des marées :
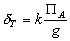 (6.43)
(6.43)
avec k un nombre de Love estimé
constant et égal à 0,6.
6.2.3 Perturbations dues aux marées
terrestres
Comme la Terre est sensible à l’attraction
astronomique, la déformation du volume terrestre induit une nouvelle
répartition des charges à l’intérieur de la Terre
ce qui entraîne une modification du champ gravitationnel terrestre.
Ce phénomène est pris en compte par une correction du potentiel
générateur. Cette correction est un potentiel 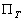 estimé
par Love [1911] :
estimé
par Love [1911] :
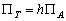 (6.44)
(6.44)
avec h un nombre de Love constant
sur l’ensemble du globe terrestre et égal à 0,3.
6.2.4 Effets de charges et d’auto-attraction
Au cours du temps, les marées océaniques
modifient la répartition des masses d’eau océaniques. Tout
comme la marée terrestre, ceci se traduit par la correction de la
dénivellation issue d’un phénomène appelé effets
de charge. Farrell [1972] fut un des premiers à étudier
l’effet des surcharges dues aux bourrelets d’eau engendrés par les
marées océaniques sur la déformation de la croûte
terrestre. En développant en harmoniques sphériques la dénivellation
relative du niveau de la mer par rapport à la position locale de
la croûte terrestre, Hendershott [1972] a montré que
la dénivellation issue des effets de charge s’écrit au point
de coordonnées 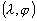 :
:
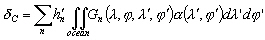 (6.45)
(6.45)
avec :
-
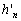 : nombre de Love pour l’ordre n
du développement en harmoniques sphériques ;
: nombre de Love pour l’ordre n
du développement en harmoniques sphériques ;
-
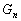 : fonction de répartition
dépendant de la position ;
: fonction de répartition
dépendant de la position ;
-
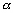 : la dénivellation de la marée
due au potentiel astronomique.
: la dénivellation de la marée
due au potentiel astronomique.
La prise en compte de cette perturbation suppose
une connaissance a priori de la marée océanique si
nous voulons garder le caractère explicite du problème. En
outre, de même que pour les marées terrestres, cette dénivellation
due aux effets de charge modifie le champ de pesanteur, ce qui amène
une autre perturbation du potentiel générateur des marées
qui se traduit sous la forme d’un potentiel d’auto-attraction [Hendershott,
1972] :
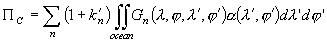 (6.46)
(6.46)
avec :
-
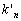 : nombre de Love pour l’ordre
n du développement en harmoniques sphériques ;
: nombre de Love pour l’ordre
n du développement en harmoniques sphériques ;
-
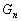 : fonction de charge de Green dépendant
de la position ;
: fonction de charge de Green dépendant
de la position ;
-
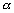 : la dénivellation de la marée
due au potentiel astronomique.
: la dénivellation de la marée
due au potentiel astronomique.
Avec cette formulation Francis et Mazzega
[1990] ont calculé des cartes mondiales du potentiel de charge qui
sont utilisées dans notre modèle, en utilisant la solution
mondiale de Schwiderski [1980c]. L’expression de la fonction de
charge 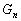 est donnée dans
leur papier.
est donnée dans
leur papier.
6.2.5 Potentiel générateur
total
Hendershott [1972], fut le premier
à prendre en compte toutes les corrections du potentiel développées
ci-dessus. Le potentiel total des marées que nous devons utiliser
dans notre étude s’écrit donc sous la forme :
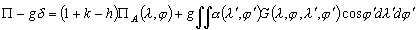 (6.47)
(6.47)
avec :
-
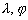 : les coordonnées géocentriques
du point considéré (longitude, latitude)
: les coordonnées géocentriques
du point considéré (longitude, latitude)
-
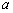 : le rayon de la Terre;
: le rayon de la Terre;
-
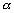 : la dénivellation de la marée
due au potentiel astronomique.
: la dénivellation de la marée
due au potentiel astronomique.
-
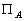 : le potentiel astronomique de marées;
: le potentiel astronomique de marées;
-
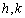 : les nombres de Love;
: les nombres de Love;
-
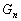 : fonction de charge de Green dépendant
de la position.
: fonction de charge de Green dépendant
de la position.
6.3 Equations du modèle hydrodynamique
6.3.1 Equations du modèle
La formulation des équations utilisées
dans le modèle hydrodynamique CEFMO a été initialisée
par Le Provost [1986] puis développée dans des travaux
ultérieurs [Le Provost et al., 1994]. Nous rappelons ici
les principales étapes de la formulation des équations hydrodynamiques
utilisées dans le modèle CEFMO. Ces équations sont
basées sur les équations littorales de la marée océanique
et projetées en coordonnées sphériques. La viscosité
horizontale est négligée et la dissipation est supposée
avoir lieu dans une couche limite mince près du fond. Les non-linéarités
provenant des termes d’advection et de dissipation sont résolues
par une méthode de perturbation. Nous obtenons ainsi un système
harmonique d’équations quasi linéarisées.
Reprenons les équations littorales
de la marée introduites dans le Chapitre 5, et tenons compte des
corrections à apporter aux forçages et à la position
absolue du fond océanique. Rappelons les différentes hypothèses
faites sur le fluide océanique qui nous conduisent aux équations
utilisées dans le modèle à savoir que ce fluide est
:
-
à réponse barotrope (c’est-à-dire que les isopressions
et les isodensités sont confondues) et de ce fait homogène
;
-
incompressible ;
-
parfait en dehors de la couche limite du fond (non visqueux , non turbulent)
;
-
régi par une loi de frottement quadratique au fond des océans
(cette loi est actuellement considérée comme modélisant
le mieux le frottement) et caractérisée par un coefficient
de type Chézy ;
-
à dimensions horizontales très grandes devant les dimensions
verticales (hypothèse des ondes longues) ;
-
à vitesse verticale très petite devant les vitesses horizontales.
Dans ce cas, l’équation de continuité
est :
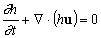 (6.48)
(6.48)
L’équation du moment dans sa forme
non conservative est :
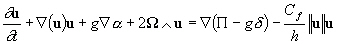 (6.49)
(6.49)
avec :
-
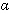 : l’élévation de surface
de l’océan ;
: l’élévation de surface
de l’océan ;
-
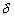 : la topographie du fond océanique
;
: la topographie du fond océanique
;
-
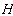 : la profondeur d’eau moyenne ;
: la profondeur d’eau moyenne ;
-
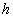 : la profondeur d’eau instantanée
(
: la profondeur d’eau instantanée
(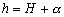 ) ;
) ;
-
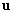 : la vitesse barotrope horizontale
;
: la vitesse barotrope horizontale
;
-
 : le potentiel global de marée
;
: le potentiel global de marée
;
-
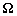 : la rotation terrestre avec le paramètre
de Coriolis
: la rotation terrestre avec le paramètre
de Coriolis 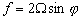 ;
;
-
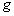 : la constante de gravité
;
: la constante de gravité
;
-
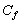 : le coefficient de friction sans
dimension de type Chézy.
: le coefficient de friction sans
dimension de type Chézy.
Dans les chapitres précédents,
la linéarisation du coefficient de frottement nous a permis d’obtenir
des relations linéaires pour les équations (6.48) et (6.49).
Or nous étudions le phénomène des marées qui
est une somme de fonctions sinusoïdales élémentaires.
A chaque fonction est associée une composante k du développement
du potentiel générateur qui a une fréquence propre 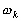 .
Nous pouvons donc résoudre les équations (6.48) et (6.49)
séparément pour chacune des composantes de la marée.
Introduisons la notation complexe associée à la fréquence
.
Nous pouvons donc résoudre les équations (6.48) et (6.49)
séparément pour chacune des composantes de la marée.
Introduisons la notation complexe associée à la fréquence 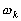 pour les différentes variables (la dénivellation et les deux
composantes de la vitesse). Pour simplifier les notations nous écrirons
pour les différentes variables (la dénivellation et les deux
composantes de la vitesse). Pour simplifier les notations nous écrirons 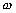 au lieu de
au lieu de 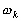 :
:
-
pour la dénivellation :
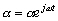 ;
;
-
pour les vitesses :
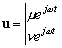 .
.
En nous plaçant en coordonnées
sphériques, à partir de (6.48) nous obtenons pour la dénivellation
:
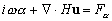 (6.50)
(6.50)
et à partir de (6.49) nous obtenons
pour les vitesses :
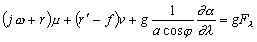 (6.51)
(6.51)
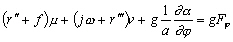 (6.52)
(6.52)
avec :
-
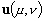 la vitesse barotrope ;
la vitesse barotrope ;
-
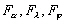 les forçages en dénivellation
dépendant de la longitude et de la latitude ;
les forçages en dénivellation
dépendant de la longitude et de la latitude ;
-
r, r’, r’’, r’’’ les coefficients de frottement exprimés dans le
Tableau 8.
|
Coefficient
|
Onde dominante
|
Autres ondes
|
|
r
|
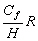
|
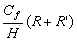
|
|
r'
|
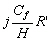
|
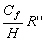
|
|
r''
|
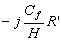
|
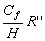
|
|
r'''
|
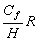
|
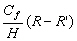
|
|
R
|
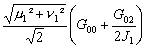
|
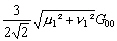
|
|
R'
|
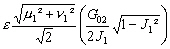
|
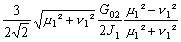
|
|
R''
|
0
|
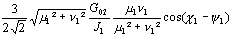
|
Tableau 8 : Expressions des coefficients de frottements quasi linéarisés
avec :
-
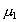 et
et 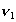 les modules des composantes de la vitesse de l’onde dominante ;
les modules des composantes de la vitesse de l’onde dominante ;
-
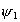 le déphasage en
le déphasage en 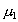 et
et 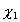 le déphasage en
le déphasage en 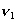 de
la vitesse de l’onde dominante ;
de
la vitesse de l’onde dominante ;
-
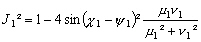 ;
;
-
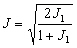 ;
;
-
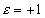 si
si 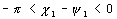 et
et 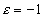 si
si 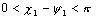 ;
;
-
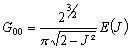 ;
;
-
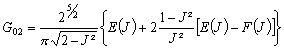 ;
;
-
E et F les intégrales de Legendre de première et deuxième
espèces.
Ces coefficients dépendent des caractéristiques
des ondes majeures d'où la nécessité d'utiliser une
méthode itérative pour résoudre le problème.
Afin de simplifier l’écriture de
(6.51) et (6.52), reprenons les notations introduites par Lyard
[1999] et posons :
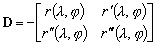 (6.53)
(6.53)
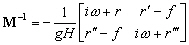 (6.54)
(6.54)
soit après inversion ( étant le déterminant de la matrice carrée M)
:
étant le déterminant de la matrice carrée M)
:
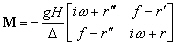 avec
avec 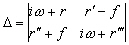 (6.55)
(6.55)
Posons 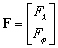 le forçage complexe de marées.
le forçage complexe de marées.
Sachant qu’en coordonnées sphériques
le gradient de la dénivellation 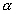 est
:
est
:
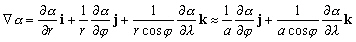 (6.56)
(6.56)
car les variations de la dénivellation
sont supposées très petites devant le rayon terrestre. Nous
déduisons de (6.51), (6.52), (6.54) et (6.56) :
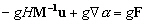
Après simplifications nous obtenons
les vitesses :
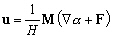 (6.57)
(6.57)
Nous pouvons alors remplacer u donnée
par (6.57) dans (6.50) :
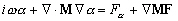 (6.58)
(6.58)
6.3.2 Système hydrodynamique
Soit 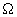 le
domaine de modélisation. Posons
le
domaine de modélisation. Posons 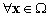 :
:
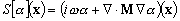 (6.59)
(6.59)
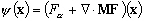 (6.60)
(6.60)
Considérant que les conditions aux
limites répondent :
-
à la condition de Neumann pour les frontières fermées
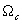 (limites imposées) ;
(limites imposées) ;
-
à la condition de Dirichlet pour les frontières
ouvertes
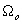 (glissement le long
des frontières).
(glissement le long
des frontières).
Le système hydrodynamique à
résoudre se résume donc par :
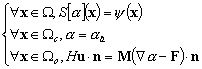 (6.61)
(6.61)
6.3.3 Expression du système
Nous allons nous intéresser plus particulièrement
à l’expression du système hydrodynamique dans le cadre de
notre étude. Nous pouvons montrer que le système (6.61) peut
s’écrire sous la forme [Le Provost and Poncet, 1978] :
 (6.62)
(6.62)
avec A, B, C, D
et F des fonctions des coefficients de frottements r, r’,
r’’
et r’’’ (cf. Tableau 8), de la fréquence 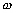 de l’onde de marée considérée, de f le paramètre
de Coriolis et de
de l’onde de marée considérée, de f le paramètre
de Coriolis et de 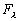 et
et 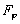 les forçages de la marée globale. L’expression de ces coefficients
est :
les forçages de la marée globale. L’expression de ces coefficients
est :
La formulation elliptique de (6.62) nous assure
l'existence et l'unicité de la solution, suivant la formulation
variationnelle proposée par Le Provost et Poncet [1978].
Mathématiquement, la résolution de ce type de problème
peut se faire par éléments finis [Le Provost and Poncet,
1978].
6.4 Résolution par les éléments
finis
6.4.1 Principe
Initiés par les travaux de Schwiderski
[1980a; 1980b; 1986], la plupart des modèles hydrodynamiques globaux
de marées océaniques sont résolus sur des grilles
éléments finis à pas constant en latitude et en longitude,
ce qui empêche un raffinement dans certaines spécifiques.
Dans notre cas, la résolution des équations définies
précédemment se fait sur des grilles éléments
finis. Dans notre cas, les éléments finis sont des triangles.
En définissant un maillage constitué de ces éléments
finis, il est possible de calculer les inconnues des équations de
la marée : la dénivellation et les deux composantes de la
vitesse de marée. De nombreux travaux préliminaires ont été
nécessaires à la mise en place de la résolution globale
de la marée par les éléments finis [Canceil,
1993; Genco, 1993; Lyard, 1992; Poncet, 1979; Rougier,
1979; Vincent, 1979].
6.4.2 Discrétisation
6.4.2.1 Maillage du domaine
Pour les calculs des solutions FES à
l’échelle globale, les équations sont résolues sur
un maillage global éléments finis. Dans un premier temps
la génération d’un maillage étant longue, nous avons
réutilisé le maillage élément finis couvrant
globalement les océans. Ce maillage fut construit aux cours de différentes
thèses [Canceil, 1993; Genco, 1993; Lyard,
1992]. Chacun des auteurs a entrepris des portions de maillage. L’assemblage
de ces différentes portions forme le maillage global (cf. Figure
45 du Chapitre 10). Les maillages ont été réalisés
avec le mailleur Trigrid [1990]. Chaque élément triangulaire
du maillage est Lagrange P2, c’est-à-dire que les dénivellations
sont calculées pour les 3 sommets des triangles ainsi que pour les
3 milieux des côtés d’un triangle, soit 6 nœuds en tout. Les
vitesses sont calculées aux 7 points de Gauss ce qui permet d’obtenir
une interpolation des vitesses et de les dériver pour en déduire
la dénivellation aux nœuds. La Figure 12 représente un des
éléments triangulaires du maillage. Les points noirs représentent
les 6 nœuds de calculs et les points rouges, les points de Gauss.
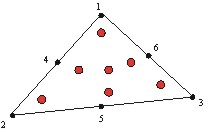
Figure 12 : Elément triangulaire
Lagrange P2
Pour bien représenter une onde de
marée, Le Provost et Vincent [1986] ont proposé un
critère local déterminant la distance maximale 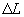 admissible entre deux nœuds du maillage :
admissible entre deux nœuds du maillage :
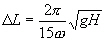 (6.63)
(6.63)
avec :
-
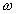 : la fréquence de l’onde de
marée considérée ;
: la fréquence de l’onde de
marée considérée ;
-
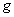 : la pesanteur supposée constante
;
: la pesanteur supposée constante
;
-
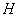 : la profondeur des fonds océaniques
au nœud de l’élément triangulaire.
: la profondeur des fonds océaniques
au nœud de l’élément triangulaire.
Ainsi, nous avons de grandes mailles pour
des eaux profondes et des mailles resserrées pour les zones littorales.
Ce critère variant peu avec la pulsation de l'onde considérée,
c’est l'onde M2 qui a été choisie pour
déterminer les tailles des mailles qui sont identiques pour toutes
les ondes. L’ordre de grandeur de la distance entre deux nœuds P2 est d’environ
10 kilomètres le long des côtes et d’environ 200 kilomètres
en plein océan.
6.4.2.2 Ressources informatiques
Etant donné le nombre de points des
maillages éléments finis, les ressources informatiques doivent
être importantes pour résoudre les équations de l’hydrodynamique.
Les calculs de la dénivellation nécessitent par conséquent
une grande place en mémoire vive et du support disque pour effectuer
les sauvegardes. C'est pourquoi tous les calculs sont effectués
sur les supercalculateurs Cray de l'IDRIS (Institut du Développement
et des Ressources en Informatique Scientifique). Cet institut fondé
en novembre 1993 est le centre majeur du CNRS pour le calcul numérique
intensif de haute performance.
Nous donnons pour information, les caractéristiques
des supercalculateurs utilisés dans le cadre de notre modélisation
hydrodynamique. Les supercalculateurs sont deux machines vectorielles Cray
dénommées C94 et C98.
-
Processeurs :
-
4 (C94) et 8 (C98) processeurs vectoriels constructeur ;
-
1 Gflops crête par processeur (375 Mflops en moyenne) ;
-
fréquence d’horloge de 250 MHz ;
-
Entier et Flottant 64 bits Cray ;
-
8 registres vectoriels de 128 mots par processeur.
-
Mémoire :
-
256/512 Mmots soit 2/4 Go utilisables par tous les processeurs ;
-
Mémoire segmentée en 256/512 bancs (accès uniforme
à mémoire).
-
Disques :
-
HOME : 14 Go (30 Mo par groupe en moyenne) ;
-
WORKDIR : 16 Go (1,4 Go par groupe) ;
-
TMPDIR : 30 Go sur C94, 60 Go sur C98 et 17 Go maxi pour un travail batch.
6.5 Bilan
Nous avons mis en place les équations
de l’hydrodynamiques appliquées aux marées. La résolution
de ces équations sur un maillage éléments finis nous
permet maintenant de produire des solutions de marées globales à
l’échelle mondiale. Notons que cette méthode de calcul a
servi de base à la production des solutions de marées FES94.1
[Le Provost et al., 1994] et FES95.2 [Le Provost et al.,
1998]. Nous allons voir dans la suite quels sont les paramètres
à réviser afin d’améliorer encore la précision
de la modélisation des marées par la méthode des éléments
finis. Ainsi, nous allons introduire la notion d’assimilation de données
afin de tenir compte des informations de terrain grâce à la
mesure marégraphique et la mesure altimétrique. En effet,
si ces données sont extrêmement intéressantes pour
la validation des modèles de marées, elles sont tout aussi
intéressantes pour l’amélioration des modèles par
l’assimilation. C’est pourquoi, dans la partie suivante, nous nous intéressons
tout particulièrement à ces types de mesures afin d’en détacher
les qualités et les défauts. Ainsi pourrons les utiliser
afin de produire nos futurs modèles.
Partie II
Observations de la marée
Back | Next
Title: Thèse de Fabien Lefèvre
Issue: Version 1.0
Date: 29/09/2000
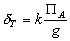 (6.43)
(6.43)
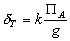 (6.43)
(6.43)
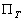 estimé
par Love [1911] :
estimé
par Love [1911] :
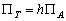 (6.44)
(6.44)
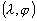 :
:
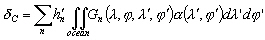 (6.45)
(6.45)
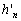 : nombre de Love pour l’ordre n
du développement en harmoniques sphériques ;
: nombre de Love pour l’ordre n
du développement en harmoniques sphériques ;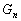 : fonction de répartition
dépendant de la position ;
: fonction de répartition
dépendant de la position ;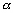 : la dénivellation de la marée
due au potentiel astronomique.
: la dénivellation de la marée
due au potentiel astronomique.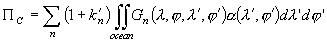 (6.46)
(6.46)
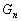 : fonction de charge de Green dépendant
de la position ;
: fonction de charge de Green dépendant
de la position ;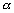 : la dénivellation de la marée
due au potentiel astronomique.
: la dénivellation de la marée
due au potentiel astronomique.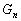 est donnée dans
leur papier.
est donnée dans
leur papier.
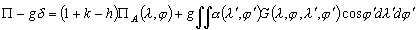 (6.47)
(6.47)
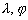 : les coordonnées géocentriques
du point considéré (longitude, latitude)
: les coordonnées géocentriques
du point considéré (longitude, latitude)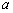 : le rayon de la Terre;
: le rayon de la Terre;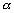 : la dénivellation de la marée
due au potentiel astronomique.
: la dénivellation de la marée
due au potentiel astronomique.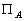 : le potentiel astronomique de marées;
: le potentiel astronomique de marées;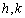 : les nombres de Love;
: les nombres de Love;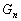 : fonction de charge de Green dépendant
de la position.
: fonction de charge de Green dépendant
de la position.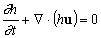 (6.48)
(6.48)
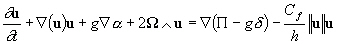 (6.49)
(6.49)
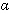 : l’élévation de surface
de l’océan ;
: l’élévation de surface
de l’océan ;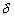 : la topographie du fond océanique
;
: la topographie du fond océanique
;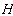 : la profondeur d’eau moyenne ;
: la profondeur d’eau moyenne ;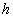 : la profondeur d’eau instantanée
(
: la profondeur d’eau instantanée
(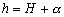 ) ;
) ;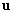 : la vitesse barotrope horizontale
;
: la vitesse barotrope horizontale
; : le potentiel global de marée
;
: le potentiel global de marée
;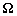 : la rotation terrestre avec le paramètre
de Coriolis
: la rotation terrestre avec le paramètre
de Coriolis 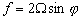 ;
;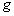 : la constante de gravité
;
: la constante de gravité
;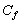 : le coefficient de friction sans
dimension de type Chézy.
: le coefficient de friction sans
dimension de type Chézy.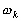 .
Nous pouvons donc résoudre les équations (6.48) et (6.49)
séparément pour chacune des composantes de la marée.
Introduisons la notation complexe associée à la fréquence
.
Nous pouvons donc résoudre les équations (6.48) et (6.49)
séparément pour chacune des composantes de la marée.
Introduisons la notation complexe associée à la fréquence 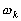 pour les différentes variables (la dénivellation et les deux
composantes de la vitesse). Pour simplifier les notations nous écrirons
pour les différentes variables (la dénivellation et les deux
composantes de la vitesse). Pour simplifier les notations nous écrirons 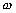 au lieu de
au lieu de 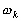 :
:
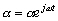 ;
;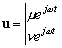 .
.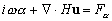 (6.50)
(6.50)
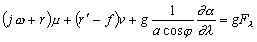 (6.51)
(6.51)
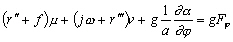 (6.52)
(6.52)
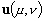 la vitesse barotrope ;
la vitesse barotrope ;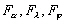 les forçages en dénivellation
dépendant de la longitude et de la latitude ;
les forçages en dénivellation
dépendant de la longitude et de la latitude ;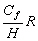
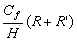
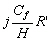
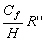
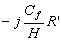
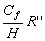
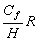
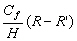
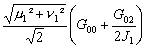
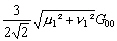
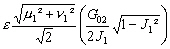
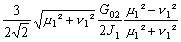
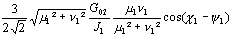
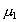 et
et 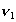 les modules des composantes de la vitesse de l’onde dominante ;
les modules des composantes de la vitesse de l’onde dominante ;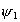 le déphasage en
le déphasage en 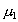 et
et 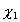 le déphasage en
le déphasage en 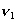 de
la vitesse de l’onde dominante ;
de
la vitesse de l’onde dominante ;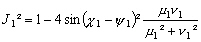 ;
;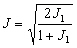 ;
;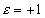 si
si 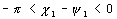 et
et 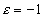 si
si 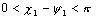 ;
;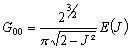 ;
;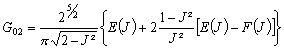 ;
;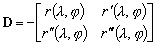 (6.53)
(6.53)
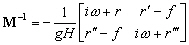 (6.54)
(6.54)
 étant le déterminant de la matrice carrée M)
:
étant le déterminant de la matrice carrée M)
:
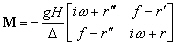 avec
avec 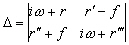 (6.55)
(6.55)
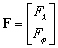 le forçage complexe de marées.
le forçage complexe de marées.
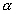 est
:
est
:
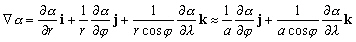 (6.56)
(6.56)
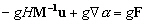
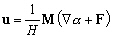 (6.57)
(6.57)
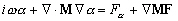 (6.58)
(6.58)
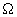 le
domaine de modélisation. Posons
le
domaine de modélisation. Posons 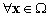 :
:
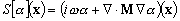 (6.59)
(6.59)
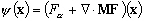 (6.60)
(6.60)
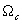 (limites imposées) ;
(limites imposées) ;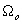 (glissement le long
des frontières).
(glissement le long
des frontières).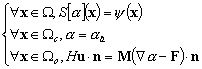 (6.61)
(6.61)
 (6.62)
(6.62)
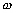 de l’onde de marée considérée, de f le paramètre
de Coriolis et de
de l’onde de marée considérée, de f le paramètre
de Coriolis et de 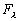 et
et 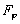 les forçages de la marée globale. L’expression de ces coefficients
est :
les forçages de la marée globale. L’expression de ces coefficients
est :
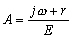 ;
;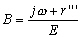 ;
;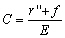 ;
;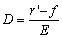 ;
;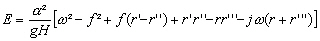 ;
;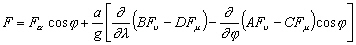 .
.
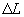 admissible entre deux nœuds du maillage :
admissible entre deux nœuds du maillage :
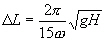 (6.63)
(6.63)
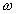 : la fréquence de l’onde de
marée considérée ;
: la fréquence de l’onde de
marée considérée ;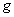 : la pesanteur supposée constante
;
: la pesanteur supposée constante
; : la profondeur des fonds océaniques
au nœud de l’élément triangulaire.
: la profondeur des fonds océaniques
au nœud de l’élément triangulaire.