
Figure 41 : Principe de mesure de la
hauteur de mer par altimétrie satellitaire (CNES)
Des méthodes très précises d’orbitographie comme la télémétrie laser ou la technique radioélectrique permettent de déterminer avec une grande exactitude la position du satellite par rapport à l’ellipsoïde de référence terrestre. La hauteur des variations du niveau de la mer se déduit donc en faisant la différence entre la distance du satellite à l’ellipsoïde et la distance mesurée par l’altimètre. Pour accéder à la mesure de la hauteur de mer (appelée topographie dynamique), il faut encore soustraire la hauteur du géoïde (cf. Figure 41, référence CNES).
Dans le domaine de la modélisation des marées océaniques, la mesure altimétrique a toujours été d’un grand apport scientifique. SEASAT fut le premier satellite dont les données furent utilisées pour en déduire une marée locale ou globale [Mazzega, 1985] suivi par le satellite GEOSAT [Cartwright, 1991; Cartwright and Ray, 1990]. Mais c’est plus particulièrement l’avènement du satellite T/P qui fut et qui est toujours scientifiquement sans précédent. Ainsi de nombreux modèles globaux de marées ont été développés depuis le lancement de T/P [Andersen, 1995; Desai and Wahr, 1995; Eanes and Bettadpur, 1996; Egbert et al., 1994; Kantha et al., 1995; Ma et al., 1994; Matsumoto et al., 1995].

Figure 41 : Principe de mesure de la
hauteur de mer par altimétrie satellitaire (CNES)
Il gravite à 1336 km d’altitude, ce qui minimise la sensibilité aux anomalies du champ de gravité ou aux effets résiduels de traînées atmosphériques. Son orbite inclinée à 66° lui permet de couvrir tous les océans situés entre les latitudes +66,039° et -66,039°. Les zones polaires ne sont pas échantillonnées. Sa période de révolution est de 9,9156 jours, ce qui permet d’avoir un bon compromis entre résolution spatiale (cf. Figure 42) et résolution temporelle. On appelle cycle l’intervalle de temps entre chaque révolution du satellite. Cependant nous verrons que cet écart de temps conduit à des problèmes d’aliasing. En effet, il y a un repliement du spectre des ondes semi-diurnes dans le spectre des longues périodes à 60 jours.
Outre les deux altimètres TOPEX et Poséïdon, l’instrumentation comprend également trois systèmes d’orbitographies et un radiomètre en vue de corriger la mesure des perturbations atmosphériques sur le signal radar. L’altimètre acquiert une mesure tous les dixièmes de secondes. Des moyennes sur 10 mesures permettent d’obtenir une valeur par seconde, soit une valeur tous les 7 km le long d’une trace.
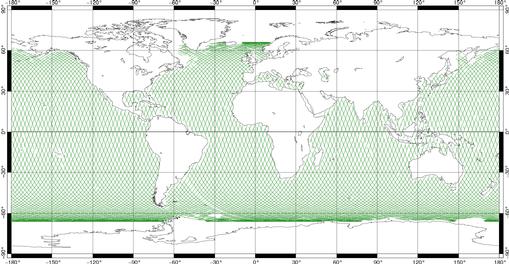
Figure 42 : Traces T/P sur la surface
océanique (cycle 126)
Plus la mer est agitée, plus sa rugosité est élevée, et plus la puissance du signal envoyé par l’altimètre est reçue faiblement par ce dernier. Les creux des vagues réfléchissent plus le signal radar que les crêtes ce qui entraîne une sous-estimation de la mesure de la hauteur de la surface instantané, d’où la nécessité de corriger les mesures en tenant compte de l’état de la mer. Il peut-être modélisé en termes de hauteur significative des vagues et de la vitesse de vent qui applique une friction à la surface de la mer [Gaspar et al., 1994].
Théoriquement, dans le cadre de l'hydrostatique, une augmentation de pression à la surface de la mer entraîne une diminution de hauteur de mer. Grossièrement, une augmentation de pression de 1 mbar entraîne une diminution de hauteur de mer de 1 cm. La pression atmosphérique locale est prise en compte par une correction de baromètre inverse.
Tout comme les masses fluides océaniques, la Terre se déforme sous l’action de la Lune et du Soleil. Ces deux astres créent des marées terrestres. Cette déformation élastique du globe solide doit être retirée de la mesure altimétrique pour accéder au signal océanique.
Plus la hauteur de mer est importante, plus la poussée exercée par la masse d’eau sur le fond océanique augmente. Cette masse d’eau va entraîner une déformation de ce fond en créant une marée de charge. Des corrections tenant compte de cette marée de charge sont aussi à appliquer.
Ainsi pour obtenir la signature des variations du niveau océanique, il faut appliquer toutes ces correction au signal altimétrique brut. C’est l’analyse de ce signal corrigé qui va nous permettre d’obtenir les composantes de la marée qui nous intéressent plus particulièrement dans le cadre de notre étude.
Sur un exemple très simple, la Figure 43 présente ce phénomène d’aliasing. Soit un signal périodique (trait foncé) de période T inférieure à la période d’échantillonnage T0 l’intervalle de temps entre deux instants de mesures échantillonnant ce signal (représenté par des points). Le signal reconstitué (trait clair) à partir de ces points sous échantillonnés conduit à un signal de période apparente Ta qui est bien supérieure à T et surtout à T0. Le sous échantillonnage du signal n’a pas permis sa reconstitution.
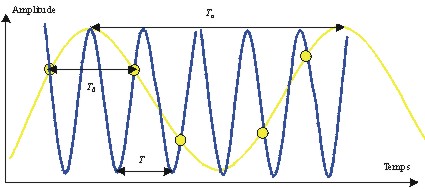
Figure 43 : Le phénomène
d’aliasing
Ainsi, dans notre cas, il y a repliement des hautes fréquences de la marée vers les basses fréquences.
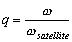 (8.68)
(8.68)
avec :
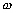 : la fréquence de l’onde considérée
;
: la fréquence de l’onde considérée
; : la fréquence de T/P.
: la fréquence de T/P.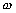 , il faut
que l’entier n vérifie :
, il faut
que l’entier n vérifie :
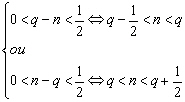 (8.69)
(8.69)
Ainsi, en résolvant (8.69), nous
pouvons calculer les périodes d’aliasing des principales ondes du
spectre pour les données de T/P (Tableau 13). La période
réelle indique la période du phénomène répétitif
de l’onde. La période aliasée est le temps minimal d’échantillonnage
de mesure pour T/P afin d’obtenir une analyse non aliasée de la
composante considérée.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 13 : Périodes d’aliasing des ondes de marées dans le signal altimétrique de T/P
Le critère de séparation
des ondes le plus communément employé est celui de Rayleigh
[Parke et al., 1987; Ponchaut, 1998]. Il permet de déterminer
la période minimale d’observation
ô necessaire à la séparation
de deux ondes de fréquences 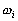 et
et 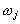 voisines :
voisines :
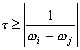 (8.70)
(8.70)
Ainsi faut-il des temps de mesures beaucoup plus longs pour pouvoir départager certaines ondes entre elles. Nous donnons dans le Tableau 14 [Smith, 1999], les périodes nécessaires pour séparer deux ondes de marées par l’analyse du signal altimétrique issu de T/P.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 14 : Période nécessaire à la séparation
des ondes de marée entre elles dans un signal T/P
(en jours)
Ainsi, nous pouvons noter qu’il faut plus de 2 ans de mesures T/P pour pouvoir séparer les composantes M2 et S2 et presque 10 ans pour K1 et Ssa. Cependant la période de T/P est intéressante car, comme le montre le Tableau 14, la plupart des ondes peuvent être séparées entre elles avec moins d’un an de mesures, ce qui explique pourquoi de nombreux modèles de marée ont pu voir le jour seulement un an après le lancement de T/P.
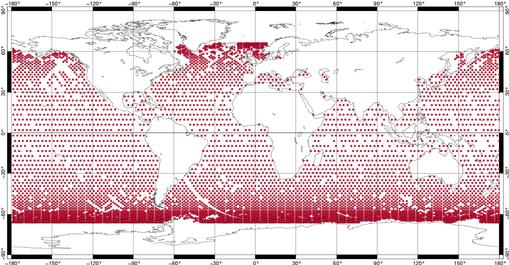
Figure 44 : Répartition des
mesures de T/P aux points de croisement (données AVISO du cycle
126)
Il est donc possible d’utiliser cette information supplémentaire pour réduire le problème de l’aliasing des hautes fréquences de la marée vers les basses fréquences. Cependant un autre problème apparaît dans ce cas, car les intervalles de temps entre un passage ascendant et le passage descendant consécutif ne sont pas constants mais sont fonctions de la latitude du point de croisement [Ponchaut, 1998; Schrama and Ray, 1994]. Pour apporter une information nouvelle entre deux de ces moments consécutifs (toujours inférieur à la demi période de T/P soit 4,958 jours), il faut que les phases de l’onde considérée sur la trace montante et la trace descendante soit le plus possible différentes. Ainsi les ondes possèdent une ou plusieurs bandes de latitude où l’étude aux points de croisement est réellement intéressante et d’autres qui n’apportent que très peu d’information supplémentaire (cf. Tableau 15, tiré de [Schrama and Ray, 1994]).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
||||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||
|
|
|
||||||||
|
|
|
||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|||||||
|
|
|
||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
||||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Tableau 15 : Déphasage des ondes aux points de croisement
Pour éviter de surcharger le Tableau 15, nous n’avons reporté que les déphasages supérieurs à 90 degrés [Ponchaut, 1998]. Ainsi, les points de croisement aux hautes latitudes n’apporteront que peu d’information dans l’étude des ondes P1 et K1, seule la bande comprise entre 46º et 64º sera d’un intérêt significatif pour les ondes K2 et S2. Pour les autres ondes, les bandes de latitudes apportant une information significative aux points de croisement sont moins explicites. Le problème de la réduction de l’aliasing aux points de croisement sera donc dépendant de l’onde considérée et de la latitude du point considéré.
Cependant, alors que seuls quelques mois de mesures marégraphiques suffisent pour obtenir une décomposition harmonique précise de l’enregistrement des variations du niveau de la mer, l’effet de l’aliasing dans l’analyse des mesures altimétriques impose que nous ayons besoin de plusieurs années pour obtenir le même spectre. De plus, la mise en place logistique est très lourde (quantité énorme de données à analyser, à corriger et à distribuer) et très coûteuse (envoi d’un satellite dans l’espace, maintenance et collecte des données).
Dans l’étude des marées, il faut donc voir la mesure satellitale comme un complément de la mesure marégraphique et non pas un remplacement. Chaque type de mesure à ses avantages et ses inconvénients. L’utilisation réfléchie de ces deux sources d’informations pour la validation et l’amélioration des modèles hydrodynamiques est un atout très important qu’il ne faut pas négliger. Dans la suite de notre travail nous allons mettre en œuvre ces deux informations de manière complémentaire afin de produire une modélisation de la marée la plus précise possible.
Partie III
Modélisation de la marée