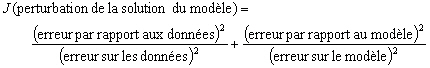
Ainsi, de manière générale, l’assimilation de données est une approche basée sur une comparaison quantitative entre un modèle et des observations. Dans le cas de la modélisation de la marée océanique, nous avons d’une part les sorties numériques de CEFMO et d’autre part des mesures extraites des marégraphes placés sur le terrain et de l’altimétrie. De ces deux sources d’informations (calculs numériques et mesures) sont tirées la mer ‘vraie’ c’est-à-dire la dénivellation réelle des océans due à la marée océanique en donnant une confiance correspondant à l’inverse de l’erreur sur ces deux sources d’informations. Dans notre cas, le modèle par éléments finis CEFMO fournit en tous les nœuds du maillage des dénivellations a priori de la marée (auxquels sont attribuées des erreurs) et les données in situ sont fournies par diverses bases de données marégraphiques et altimétriques (auxquelles sont attribuées des barres d’erreurs).
L’assimilation de données utilisée dans notre étude est basée sur une technique d’inversion avec une approche de type moindres carrés. Cette approche revient à chercher la perturbation du modèle qui minimise une fonction coût J :
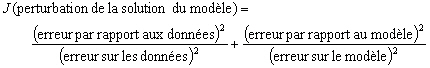
Dans le domaine de l’océanographie appliquée aux marées, cette technique a commencé à être développée à la fin des années 70 [Bennett and McIntosh, 1982]. En effet, bien que les marées soient certainement le phénomène océanique le plus prévisible, que les constantes harmoniques du spectre soient connues et calculées le long de la plupart des côtes et des îles du globe terrestre et que les équations régissant la dynamique des marées soient établies depuis Laplace (fin du 18ème siècle), l’acquisition de données marégraphiques en zone pélagique est récente. Il a fallut attendre l’avancée technologique de mesures du niveau de la surface en plein océan (marégraphes de grands fonds) pour obtenir une base de données des composantes du spectre de marée bien distribuées parmi les océans. En outre, les années 90 ont vu l’essor de l’exploration satellitaire par des satellites tels TOPEX/Poséidon ou ERS1 qui ont permis de fournir des relevés altimétriques du niveau de la mer sans précédent en matière de densité spatiale. Les mesures satellitales et les mesures marégraphiques apportent donc de précieuses et nombreuses informations qui, au lieu d’être uniquement utilisées comme bases de comparaisons quantitatives peuvent être aussi incorporées dans les modèles numériques de marées pour les améliorer. De nombreuses méthodes d’assimilation ont alors été mise en place pour améliorer la modélisation globale de la marée [Egbert and Bennett, 1996; Jourdin, 1992; Jourdin et al., 1991; Zahel, 1991 ].
Les erreurs sur le modèle sont dues principalement :
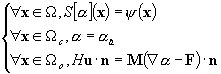(9.71)
Ce système est résolu par la technique de discrétisation en élément finis (éléments triangulaires, approximation en Lagrange P2). La solution de ce système sera appelée solution a priori.
Dans la suite nous prenons comme notation :
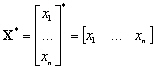
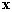un vecteur de dimension N et 
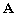une matrice symétrique de dimension NxN. Le scalaire 
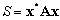est appelé forme quadratique.
Soit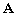 
une matrice de dimension NxN. 
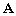est dite matrice hermitienne si et seulement si :
(9.72)
Une des propriétés fondamentales
de la matrice 
est que la transposée
du conjugué de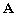 
est égal
à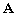 
:
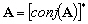(9.73)
Soit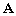 
une matrice hermitienne de dimension NxN. 
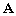est dite matrice hermitienne définie positive si et
seulement si :
(9.74)
Une variable aléatoire est une variable X qui prend une valeur donnée avec une probabilité donnée.
La fonction de répartition associée à une variable aléatoire X est :
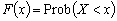(9.75)
La densité de probabilité associée à une variable aléatoire X est :
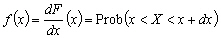(9.76)
L’espérance mathématique
E est la somme des produits de toutes les valeurs distinctes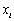 
que peut prendre X, multipliées par leurs probabilités respectives 
:
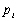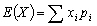(9.77)
Si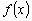 
est continue et intégrable :
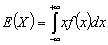(9.78)
La variance d’une variable aléatoire est définie par :
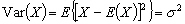(9.79)
L’écart-type est alors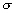 
.
La covariance de deux fonctions aléatoires est définie par :
(9.80)
La matrice de covariance
d’un vecteur de variables aléatoires 
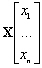est :
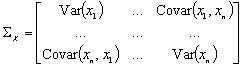(9.81)
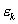représentant l’erreur de mesure du kième site
d’observation de donnée in situ :
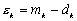(9.82)
avec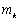 
la valeur de la dénivellation réelle et 
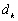le meilleur estimateur non-biaisé de l’observation (mesure marégraphique
in situ).
On définit de même une fonction de covariance d’erreur pour les observations :
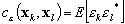(9.83)
ainsi qu’une matrice de covariance d’erreur pour les N données mesurées :
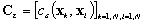(9.84)
les valeurs réelles du forçage, de la dénivellation
sur les frontières ouvertes et le flux des vitesses sur les frontières
fermées. Nous définissons les erreurs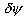 
, 
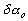et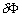
:
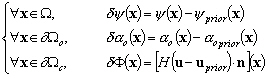(9.85)
Ainsi, le champ de dénivellation qui résulte de cette considération des erreurs est donné par :
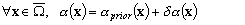(9.86)
Comme le système S défini en (9.71) est linéaire, l’erreur sur la dénivellation est donnée par:
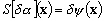(9.87)
Nous considérerons par la suite
que 
est un triplet de trois
champs de variables aléatoires indépendantes. La solution
assimilée est définie par la réalisation de ces trois
variables qui minimise une fonction coût. Nous supposons que les
erreurs statistiques sont approximativement décrites par leurs fonctions
de covariance d’erreur :
(9.88)
où E est l’espérance mathématique.
Nous définissons ensuite pour chacune
des erreurs du modèle, les opérateurs linéaires de
covariances agissant sur le champ de dénivellation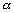 
:
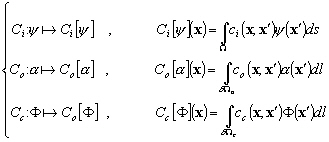(9.89)
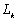la fonction linéaire qui à l’observation 
,
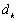mesurée au point 
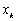, projette
le champ de dénivellation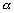 
dans l’espace des observations. C’est en fait l’interpolation du champ 
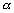au point 
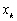de la mesure in situ.
Soit 
le vecteur des différences entre la mesure 
à un point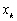 
et le champ 
interpolé
au point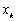 
:
(9.90)
Nous définissons alors la fonction
coût 
pour les observations
:
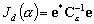(9.91)
Supposons que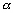 
soit distribué suivant une loi normale. La densité de probabilité
pour que les observations in situ du champ 
coïncident avec la mesure de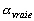 
est donnée par :
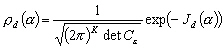(9.92)
Dans la pratique, nous supposons que les
données ne sont pas corrélées entre elles. Cette hypothèse
est justifiée par le fait que l’erreur de mesure d’un marégraphe
n’influe aucunement sur la mesure d’un autre marégraphe. La matrice
de corrélation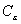 
est donc
une matrice diagonale composée des variances sur les erreurs des
données. La matrice inverse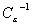 
représente la confiance que nous attribuons à chacune de
ces données.
pour le modèle
au moyen des opérateurs de covariances introduits en (9.89) suivant
une approche développée par Tarantola [1987] :
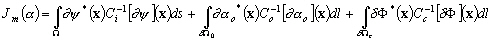(9.93)
La densité de probabilité
pour qu’un triplet de paramètres du modèle coïncide
avec la mesure de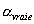 
est donnée
par :
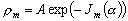(9.94)
où A est un facteur de normalisation.
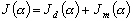(9.95)
La dénivellation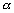 
qui
minimise cette fonction coût est la solution la plus cohérente
à la fois des observations et la de la solution a priori proposé
par le modèle. Ainsi,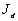 
donne une indication sur la meilleure estimation de l’ensemble des observations 
par rapport à la dénivellation vraie aux sites d’observations.
La densité de probabilité
pour qu’un triplet de paramètres du modèle et pour que les
observations in situ du champ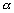 
coïncide avec la mesure de 
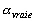est donnée par :
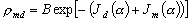(9.96)
où B est un facteur de normalisation.
Cependant, nous ne connaissons qu’approximativement les fonctions de covariances. De plus, si le nombre de nœuds du maillage est important, il faut inverser des matrices de covariances de très grandes dimensions, ce qui est numériquement très lourd. Nous avons donc utilisé la technique des représenteurs qui permet de résoudre ces problèmes.
Soit 
l’espace des dénivellations possibles de marées. La fonction
coût définie en (9.95) est une forme quadratique définie
positive. Nous pouvons donc définir un produit scalaire dans l’espace
des dénivellations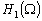 
:
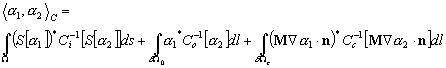(9.97)
Ce produit scalaire contient toute l’information associée à l’erreur sur le modèle. La fonction coût s’exprime alors selon :
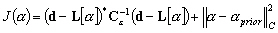(9.98)
Sous certaines hypothèses de régularité
des opérateurs de covariances,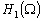 
est un espace de Hilbert (c’est-à-dire que les dénivellations
sont carrée-intégrables sur W).
Donc, d’après le théorème de Riesz, puisque
Lk est une fonctionnelle linéaire, il existe un
champ rk dans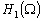 
tel que :
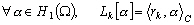(9.99)
rk est appelé représenteur associé à la fonctionnelle Lk [Egbert and Bennett, 1996; Yosida, 1980].
En supposant que les représenteurs
sont linéairement indépendants, ils forment une base de vecteurs
de l’espace vectoriel V de dimension K, où K est le nombre
de mesures in situ que nous voulons assimiler. Ainsi tous les champs de
l’espace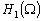 
peuvent s’exprimer
sous la forme :
(9.100)
où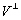 
est l’espace vectoriel orthogonal à V. L’espace de dimension
infinie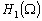 
est la réunion
de V et 
. Les propriétés
des sous-espaces vectoriels orthogonaux (norme d’une somme égale
à la somme de la norme et produit scalaire d’un vecteur orthogonal
nul) nous permettent d’écrire :
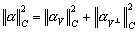(9.101)
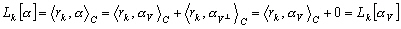(9.102)
Ainsi, le terme orthogonal de (9.99) ne modifie pas le premier membre de la fonction coût. Nous pouvons le choisir de telle manière qu’il soit égal au champ zéro pour qu’il minimise le terme de droite de la fonction coût (9.97). Nous recherchons la solution sous la forme de combinaison linéaire de représenteurs, c’est-à-dire :
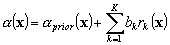(9.103)
Posons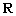 
la
matrice hermitienne des produits scalaires des représenteurs :
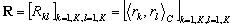(9.104)
Les principales caractéristiques des composantes de cette matrice sont :
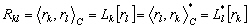(9.105)
Le problème, initialement de dimension infinie, est devenu de dimension finie K, le nombre de mesures in situ à assimiler (nombre de degrés de liberté). Nous avons donc :
(9.106)
La fonction coût se simplifie en :
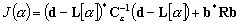(9.107)
Le vecteur b qui minimise (9.107) est solution du système KxK :
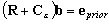(9.108)
Les représenteurs sont calculés en résolvant (9.108) et la solution en dénivellation est calculée en résolvant (9.99). La matrice de covariance d’erreurs associée à la solution assimilée est :
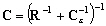(9.109)
La matrice de covariance a posteriori est très intéressante pour diagnostiquer l’assimilation. Elle nous permet de diagnostiquer la cohérence entre la covariance a priori des observations et celle du modèle.