Chapitre 10 Un modèle indépendant de la
mesure altimétrique : FES98
10.1 Présentation du chapitre
Au milieu des années 90, les solutions
FES94.1 et FES95.2 offraient à la communauté scientifique
des nouveaux types de solutions globales de marées. Dans la continuité
des améliorations sans cesse réalisées sur les modèles
FES (Finite Element Solution), nous sommes à même de calculer
une nouvelle solution globale qui tient compte des apports de l’assimilation
de données grâce à la méthode des représenteurs
introduite dans le chapitre précédent. Cette méthode
d’assimilation va nous permettre d’inclure les informations de terrain
dans notre modèle afin de produire de nouvelles solutions pour les
principales ondes du spectre de marée. En premier lieu dans ce chapitre,
nous mettrons en place les améliorations à apporter au modèle
hydrodynamique. Puis nous quantifierons les solutions hydrodynamiques obtenues.
Enfin, nous utiliserons la méthode d’assimilation basée sur
les représenteurs pour améliorer nos solutions en dénivellation,
au moyen de données marégraphiques. Nous produirons ainsi
des solutions de qualité en zones côtières et sur les
plateaux tout en étant indépendant de la mesure altimétrique.
Les nouvelles solutions seront nommées FES98.
10.2 Calcul des solutions hydrodynamiques
libres
10.2.1 Division du maillage
Pour les calculs des solutions FES à
l’échelle globale, les équations sont résolues sur
un maillage global éléments finis. La génération
d’un maillage est longue et coûteuse en temps de calcul. Un des buts
premiers dans cette étude étant de vérifier le code
d’assimilation sur une couverture globale, nous avons réutilisé
le maillage élément finis couvrant globalement les océans
et utilisé pour calculer les solutions FES94.1 et FES95.2 (cf. Figure
45). Nous avons préféré refaire un maillage beaucoup
plus précis ultérieurement. Une augmentation immédiate
de la précision aurait apporté de trop nombreux problèmes
informatiques à résoudre simultanément avec le débuggage
du code d’assimilation.
Malgré tout, la taille du maillage
est trop grande pour permettre une résolution globale. Il a donc
été divisé en plusieurs sous domaines (les noms entre
parenthèses sont les termes génériques des bassins
utilisés dans le code) :
-
l’océan Arctique (ARCTIC) ;
-
l’Atlantique Nord (ATLNORD) ;
-
l’Atlantique Sud (ATLSUD) ;
-
la baie d’Hudson (HUDSON) ;
-
l’océan Indien (INDIEN) ;
-
les mers de la Malaisie (MALAYSIE) ;
-
la mer Méditerranée (MEDITER) ;
-
le Pacifique Nord (PACNORD) ;
-
le Pacifique Sud (PACSUD).
Nous donnons dans le Tableau 16 les différentes
caractéristiques des bassins en termes numériques. Ces données
sont essentielles pour la résolution du modèle. Elles permettent
de dimensionner tous les paramètres et les tableaux numériques
qui interviennent au cours des calculs. En effet pour nous affranchir au
maximum de tous les problèmes de débordements de tableaux
(véritables fléaux du programmeur…) au cours de l’exécution
du code CEFMO, toutes nos déclarations de tableaux sont statiques
et non dynamiques.
Figure 45 : Maillage global pour le
calcul des solutions FES94.1, FES95.2 et FES98
|
Bassin
|
Nombre d’éléments triangulaires
|
Nombres de nœuds en Lagrange-P2
|
Nombre de conditions aux limites ouvertes en Lagrange-P2
|
|
ARCTIC
|
18 787
|
41 858
|
100
|
|
ATLNORD
|
16 129
|
3 5695
|
211
|
|
ATLSUD
|
20 585
|
43 817
|
171
|
|
HUDSON
|
3 315
|
7 564
|
17
|
|
INDIEN
|
18 695
|
40 804
|
276
|
|
MALAYSIE
|
14 787
|
31 556
|
251
|
|
MEDITER
|
11 350
|
23 998
|
5
|
|
PACNORD
|
20 897
|
45 913
|
280
|
|
PACSUD
|
20 044
|
43 487
|
250
|
|
Total
|
144 589
|
314 692
|
1 561
|
Tableau 16 : Caractéristiques numériques des différents
bassins océaniques utilisés dans CEFMO
Dans un premier temps, tous les calculs
se font indépendamment pour chaque bassin.
10.2.2 Résolution numérique
Les calculs des solutions de marées
sont effectués sur les supercalculateurs CRAY de l’IDRIS par la
soumission de jobs en batch. Les solutions sont assemblées sur des
stations de travail Sun Ultra 1. Afin de faciliter et d’automatiser les
calculs, un script de soumission a été établi au niveau
mondial. Pour calculer les ondes M2 et K1,
les calculs se décomposent en quatre étapes principales :
-
Etape 1 (2 calculs en tout) :1 calcul en mode dominant pour chacune
des ondes M2 et K1 et pour chacun des
9 bassins ;
-
Etape 2 (8 calculs pour tous les bassins à part HUDSON avec
20 calculs) : 4 calculs en mode mixte pour chacune des ondes M2
et K1 et pour chacun des 9 bassins;
-
Etape 3 (1 calcul) : 1 calcul avec sauvegarde des réponses
impulsionnelles pour l’onde M2 ou K1
et pour chacun des 9 bassins;
-
Etape 4 (1 calcul) : 1 calcul d’assemblage par une résolution
par blocs des solutions sur chacun des bassins (réponse libre).
Pour calculer les ondes S2,
N2,
K2,
2N2, O1, et Q1 les
calculs se décomposent en deux parties principales :
-
Etape 1 (1 calcul) :1 calcul utilisant les coefficients de frottement
calculé pour les ondes M2 et K1
avec sauvegarde des réponses impulsionnelles pour chacun des 9 bassins
;
-
Etape 2 (1 calcul) : 1 calcul d’assemblage par une résolution
par blocs des solutions sur chacun des bassins (réponse libre).
10.2.3 La résolution par blocs
10.2.3.1 Principe
Le calcul d’une solution de marée au
niveau global est coûteux en temps de calcul et en place mémoire.
Les ordinateurs actuels ne permettent pas de calculer une solution globale
de marée sur le maillage global éléments finis que
nous avons considéré. C’est pourquoi, en prenant en compte
les caractéristiques des moyens informatiques mis à notre
disposition par l’IDRIS, le maillage de la surface océanique a été
divisé en plusieurs sous domaines. Les solutions sont calculées
indépendamment les unes des autres sur chacun des sous domaines
en imposant des conditions aux limites aux frontières partagées.
Pour chaque bassin ces frontières partagées sont des frontières
ouvertes et les côtes représentent les frontières fermées.
Puis, par la linéarité du modèle, une résolution
finale utilisant les calculs effectués pour chacun des sous domaines,
permet d’assembler la solution globale. Nous reprenons et expliquons de
manière plus approfondie cette méthode développée
initialement par Lyard [1998].
10.2.3.2 Système par blocs
Considérons le problème global
obtenu en additionnant N-1 bassins océaniques séparés.
Les inconnues sont triées par bassin sauf les inconnues qui sont
à la frontière de deux bassins différents. Ces inconnues
partagées sont assemblées dans un Nième
vecteur : elles appartiennent toutes à des frontières ouvertes.
Par ce formalisme, le modèle hydrodynamique global des N-1
bassins est équivalent au système :
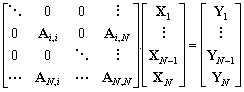 (10.110)
(10.110)
avec :
-
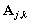 : les matrices de coefficients fixés
par les équations hydrodynamiques et imposant les dépendances
entre les nœuds du maillage ;
: les matrices de coefficients fixés
par les équations hydrodynamiques et imposant les dépendances
entre les nœuds du maillage ;
-
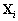 : les vecteurs d’inconnues strictement
à l’intérieur du bassin i ;
: les vecteurs d’inconnues strictement
à l’intérieur du bassin i ;
-
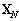 : le vecteur d’inconnues partagées
entre deux bassins (pour tous les N-1 bassins) ;
: le vecteur d’inconnues partagées
entre deux bassins (pour tous les N-1 bassins) ;
-
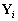 : le forçage total appliqué
sur le bassin océanique i ;
: le forçage total appliqué
sur le bassin océanique i ;
-
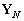 : le forçage total appliqué
sur les frontières ouvertes partagées.
: le forçage total appliqué
sur les frontières ouvertes partagées.
De (10.110) nous pouvons déduire :
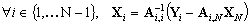 (10.111)
(10.111)
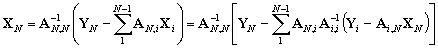 (10.112)
(10.112)
10.2.3.3 Solution a priori : système
contraint
Dans notre cas, nous cherchons à retirer
l’action du forçage que nous imposons par des conditions aux limites
sur les frontières ouvertes de l’ensemble des bassins. Nous voulons
obtenir une solution globale qui n’a plus d’interdépendance fixée
par ces conditions aux limites entre les différents bassins du domaine
global. Ainsi, notre but est de calculer la part des solutions de marée
qui est due aux forçages (que nous imposons a priori sur les frontières
ouvertes) et la part du forçage naturel (pour simplifier nous emploierons
le terme de forçage naturel pour désigner le forçage
astronomique plus le forçage des effets secondaires). Comme le système
est linéaire, si nous retirons l’influence de ces conditions aux
limites imposées sur les frontières ouvertes, nous accéderons
aux solutions purement hydrodynamiques qui ne sont que la conséquence
du forçage naturel.
Notre système hydrodynamique est
linéaire, donc nous pouvons chercher les vecteurs 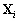 sous la forme :
sous la forme :
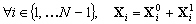 (10.113)
(10.113)
avec :
-
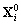 : les vecteurs d’inconnues strictement
à l’intérieur du bassin i et qui ne sont que la conséquence
du forçage naturel ;
: les vecteurs d’inconnues strictement
à l’intérieur du bassin i et qui ne sont que la conséquence
du forçage naturel ;
-
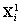 : les vecteurs d’inconnues strictement
à l’intérieur du bassin i et qui ne sont que la conséquence
du forçage imposé par nos conditions aux limites ;
: les vecteurs d’inconnues strictement
à l’intérieur du bassin i et qui ne sont que la conséquence
du forçage imposé par nos conditions aux limites ;
10.2.3.4 Système libre
Les vecteurs qui nous intéressent sont
les vecteurs 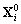 car ils sont exempts
de l’influence des conditions aux limites qui nous permettent a priori
d’assurer le calcul des solutions de marées sur chaque sous domaine
et la continuité entre les sous domaines du maillage de l’océan
mondial.
car ils sont exempts
de l’influence des conditions aux limites qui nous permettent a priori
d’assurer le calcul des solutions de marées sur chaque sous domaine
et la continuité entre les sous domaines du maillage de l’océan
mondial.
Ainsi, d’après (10.110) le système
a priori sans condition aux limites imposée s’écrit :
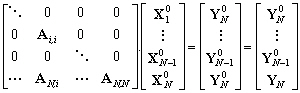 (10.114)
(10.114)
Nous n’avons plus de dépendance
en 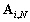 puisque les conditions aux
limites sont nulles dans le calcul des
puisque les conditions aux
limites sont nulles dans le calcul des 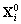 .
Nous ne considérons que la part du forçage astronomique.
Nous en déduisons :
.
Nous ne considérons que la part du forçage astronomique.
Nous en déduisons :
 (10.115)
(10.115)
et,
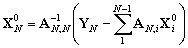 (10.116)
(10.116)
Soit :
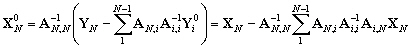 (10.117)
(10.117)
10.2.3.5 Système de perturbation
Les vecteurs 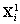 peuvent être considérés comme des perturbations de
la solution libre. En effet, ils représentent la contribution dans
la solution forcée des conditions aux limites forcées, sans
influence du potentiel naturel. Ainsi, d’après (10.110) le système
qui est l’unique conséquence des conditions aux limites imposées
s’écrit :
peuvent être considérés comme des perturbations de
la solution libre. En effet, ils représentent la contribution dans
la solution forcée des conditions aux limites forcées, sans
influence du potentiel naturel. Ainsi, d’après (10.110) le système
qui est l’unique conséquence des conditions aux limites imposées
s’écrit :
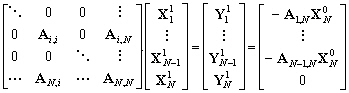 (10.118)
(10.118)
En effet, il n’y a pas de dépendance
autres sur les frontières :
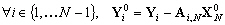 (10.119)
(10.119)
10.2.3.6 Réduction des matrices
d’inversion
La technique de résolution par blocs
consiste à éliminer les vecteurs 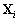 de
(10.112). En reportant, les valeurs des vecteurs
de
(10.112). En reportant, les valeurs des vecteurs 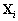 données par (10.111) dans (10.112) pour tous les indices i
variant de 1 à N1, nous obtenons après simplifications
:
données par (10.111) dans (10.112) pour tous les indices i
variant de 1 à N1, nous obtenons après simplifications
:
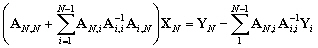 (10.120)
(10.120)
Il nous faut maintenant résoudre
(10.120) pour déterminer 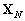 .
Le problème ici est que cette résolution implique le calcul
de l’inverse de la matrice globale
.
Le problème ici est que cette résolution implique le calcul
de l’inverse de la matrice globale 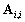 ce qui est impossible étant donnée la taille de cette matrice.
Le calcul direct est donc compromis. Il faudrait utiliser une résolution
itérative, lourde et coûteuse pour résoudre (10.120).
ce qui est impossible étant donnée la taille de cette matrice.
Le calcul direct est donc compromis. Il faudrait utiliser une résolution
itérative, lourde et coûteuse pour résoudre (10.120).
Cependant, nous remarquons que la matrice
inverse 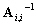 est multipliée
par des matrices
est multipliée
par des matrices 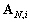 et
et 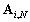 telles que tous les coefficients de la matrice inverse ne sont pas nécessaires.
En effet, les matrices
telles que tous les coefficients de la matrice inverse ne sont pas nécessaires.
En effet, les matrices 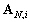 et
et 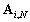 ne contiennent que des coefficients d’équations ne faisant intervenir
que les nœuds frontières et les nœuds auxquels ils sont connectés,
c’est-à-dire les nœuds voisins de ces nœuds frontières. Les
inconnues strictement intérieures d’un bassin i peuvent être
séparées en deux groupes :
ne contiennent que des coefficients d’équations ne faisant intervenir
que les nœuds frontières et les nœuds auxquels ils sont connectés,
c’est-à-dire les nœuds voisins de ces nœuds frontières. Les
inconnues strictement intérieures d’un bassin i peuvent être
séparées en deux groupes :
-
le groupe 1 qui contient les inconnues qui n’ont pas de relations directes
avec les inconnues aux frontières ;
-
le groupe 2 qui contient les nœuds voisins des inconnues aux frontières
ouvertes.
En classant les inconnues des bassins suivant
le groupe 1 et le groupe 2, nous avons :
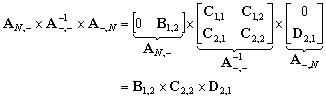 (10.121)
(10.121)
Introduisons la notation ~ qui indique
que les vecteurs ou les matrices sont réduits à leurs seuls
blocs en relation avec les inconnues du bassin océanique i.
Le problème avec conditions aux limites imposées devient
:
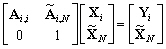 (10.122)
(10.122)
Nous avons alors :
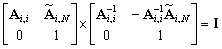 (10.123)
(10.123)
Si nous distinguons les deux groupes d’inconnues
strictement intérieures, il vient :
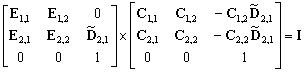 (10.124)
(10.124)
Le terme 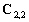 est
dimensionné par le carré du nombre de nœuds qui sont voisins
d’au moins un nœud partagé sur une frontière ouverte. Ce
terme peut être calculé par les matrices inverses déduites
du problème a priori (méthode de réponse impulsionnelle)
sur chacun des bassins.
est
dimensionné par le carré du nombre de nœuds qui sont voisins
d’au moins un nœud partagé sur une frontière ouverte. Ce
terme peut être calculé par les matrices inverses déduites
du problème a priori (méthode de réponse impulsionnelle)
sur chacun des bassins.
Une fois que nous avons calculé
les termes 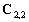 , nous en déduisons
les termes
, nous en déduisons
les termes 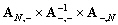 . Puis nous pouvons
calculer
. Puis nous pouvons
calculer 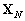 à partir de
(10.120). Une fois que nous avons calculé le vecteur
à partir de
(10.120). Une fois que nous avons calculé le vecteur 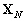 ,
nous pouvons le reporter dans (10.117), ce qui nous donne le vecteur
,
nous pouvons le reporter dans (10.117), ce qui nous donne le vecteur 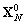 .
De là nous en déduisons les vecteurs
.
De là nous en déduisons les vecteurs 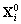 .
Nous avons ainsi résolu le problème de détermination
des inconnues aux frontières ouvertes.
.
Nous avons ainsi résolu le problème de détermination
des inconnues aux frontières ouvertes.
10.2.3.7 Calcul
Si les solutions sont contraintes par les
conditions aux limites 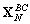 aux
frontières ouvertes, alors la solution vectorielle des nœuds partagés
est donnée par :
aux
frontières ouvertes, alors la solution vectorielle des nœuds partagés
est donnée par :
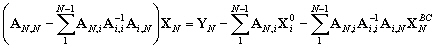 (10.125)
(10.125)
Une fois que le problème de détermination
des inconnues aux frontières ouvertes est résolu, nous pouvons
calculer les inconnues intérieures de chaque domaine grâce
à la formule :
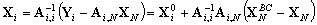 (10.126)
(10.126)
Ainsi, nous obtenons les solutions libres
de notre système hydrodynamique.
10.2.4 Outils de comparaison
Pour évaluer la qualité des
nouvelles solutions FES98, les comparaisons ont été faites
avec des banques de données de différentes origines (marégraphie
et altimétrie) et la RMS introduite dans le paragraphe 7.4 et dont
nous rappelons l’expression:
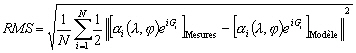 (10.127)
(10.127)
avec :
-
 la norme telle que pour un complexe
:
la norme telle que pour un complexe
: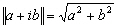 ;
;
-
N le nombre d’observations ;
-
i l’indice sur les observations ;
-
a i l’amplitude du point d’indice i ;
-
Gi la phase du point d’indice i.
De plus, afin de rendre compte globalement
de la qualité des solutions (en prenant en compte toutes les ondes
calculées), nous introduisons une Root Sum Square (RSS) :
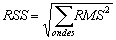 (10.128)
(10.128)
10.2.5 Calcul des solutions forcées
et libres
Avant de calculer de nouvelles solutions globale
de marée sur notre maillage éléments finis, nous avons
révisé quelques paramètres d’entrée de notre
modèle par rapport aux calculs des solutions précédentes
FES94.1 et FES95.2.
10.2.5.1 Conditions aux limites
Comme nous l’avons vu plus haut, il n’est
pas possible de calculer d’un seul bloc les solutions de marées
à une échelle globale. Le calcul se fait sur chacun des 9
sous domaines. L’assemblage de ces sous domaines constituera la solution
globale. Pour les calculs, il faut donc imposer des conditions aux limites
fermées pour les points des maillages qui sont sur des côtes
et des conditions limites ouvertes pour les points des maillages qui sont
frontières avec un autre maillage (dernière colonne du Tableau
16). Les conditions aux limites fermées imposent un flux de vitesse
nul aux frontières du domaine considéré. Les conditions
aux limites ouvertes sont imposées par le modèle de marée
CSR3.0 [Eanes and Bettadpur, 1996]. Au moment de nos calculs, ce
modèle était considéré par la communauté
scientifique comme un des meilleurs modèles globaux de marée
particulièrement en plein océan [Shum et al., 1997].
Les solutions obtenues dans ce cas sont appelées solutions forcées.
Nous verrons dans la suite que ces conditions aux limites ne sont utilisées
que pour assurer une convergence plus rapide des solutions au cours du
calcul itératif. En effet grâce à un ultime calcul,
du fait de la linéarité des équations, il est possible
de retirer l’influence de ces conditions aux limites grâce à
la méthode de résolution par blocs introduite dans le paragraphe
10.2.3.
10.2.5.2 Mode de calcul
Dans le cas des zones littorales, l’hypothèse
d’une onde M2 dominante n’est plus vérifiée
partout (exemple de l’océan Arctique [Lyard, 1997] et de
la Mer Jaune [Lefèvre et al., 1999c]). Nous avons donc effectué
tous nos calculs suivant un mode dit ‘combin’é. Ce mode tient compte
de l’effet de deux ondes dominantes dans le calcul des coefficients de
frottement au cours des itérations effectuées dans le code
CEFMO. Ainsi, nous avons considéré que l’onde M2
est dominante dans certaines zones de l’océan mondial et que par
complémentarité, l’onde K1 l’est dans les
autres.
10.2.5.3 Bathymétrie
La base de données ETOP05 [National
Geographic Data Center, 1987] a été complétée
sur les plateaux continentaux et des mers particulières comme la
Mer de Ross ou la Mer de Weddell [Le Provost et al., 1994]. Ces
améliorations sont le fruit d’études locales basées
sur des fonds de cartes et des collectes de points de sondes. La bathymétrie
a été projetée sur nos grilles éléments
finis.
10.2.5.4 Effets de charges et d’auto-attraction
Pour FES94.1 des cartes globales des effets
de charges et d’auto-attraction avaient été calculées
par Francis et Mazzega [1990] en se basant sur les solutions de
Schwiderski
[1980c]. Mais la résolution de ces dernières n’est que de
1x1 degrés. De nouvelles cartes ont été calculées
à partir de la solution de marée CSR3.0 (Francis,
communication personnelle, 1995), avec une résolution de 0,5x0,5
degrés. Une résolution plus fine apporte donc une meilleure
prise en considération des gradients. La résolution de ces
effets de charge près des côtes, là où la dissipation
énergétique est la plus forte, est donc elle aussi améliorée.
Afin de bien rendre compte de l’amélioration apportée entre
les anciennes cartes et les nouvelles cartes de charges et d’auto-attraction,
nous donnons Figure 46 la différence des deux solutions citées
précédemment. Comme nous pouvons le voir, des différences
supérieures au centimètre sont présentes au milieu
de l’océan Atlantique, et de plus de 2 cm dans certaines mers littorales
comme la Mer de Weddell, la Baie de l’Hudson, la Mer d’Irlande…
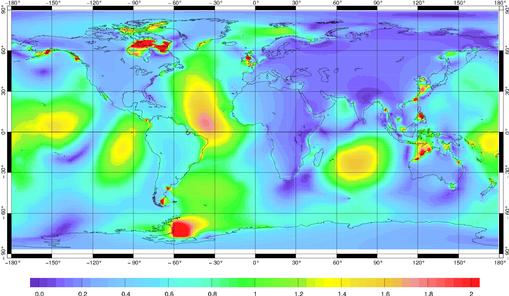
Figure 46 : Différences entre
les anciens effets de charges et d’auto-attraction basés sur les
solutions de marées de Schwiderski et ceux basés sur CSR3.0
10.2.5.5 Coefficients de frottement
Dans le modèle de résolution
par éléments finis, le coefficient de frottement est paramétrisé
par une loi quadratique. Un coefficient de type Chézy est utilisé
empiriquement dans la modélisation. Ce coefficient a été
déterminé par des études sur le plateau continental
européen. Etant essentiel à la bonne représentation
de la dissipation et donc à la bonne qualité de nos solutions,
nous avons entrepris plusieurs simulations avec des coefficients de Chézy
différents afin de déterminer si, d’une part, la valeur habituellement
utilisée est optimale à l’échelle globale, et si,
d’autre part, cette valeur n’est pas différente suivant les bassins
océaniques. La valeur communément prise à l’échelle
de calculs globaux étant 3x10-3, nous avons effectué
différentes simulations globales autour de cette valeur avec 6 coefficients
de frottement différents :
-
2x10-3 ;
-
2,5x10-3 ;
-
3x10-3 ;
-
3,5x10-3 ;
-
4x10-3 ;
-
5x10-3 ;
afin de dégager une valeur seuil optimale.
Pour comparer les différentes solutions
calculées nous avons eu recours à la base de données
marégraphiques ST95 introduite dans le paragraphe 7.4. Nous avons
calculé les différentes RMS des solutions hydrodynamiques
libres, c’est-à-dire qui n’ont subit aucun forçage (Tableau
5).
|
Coefficient de frottement
|
RMS (cm)
|
|
2x10-3
|
13,22
|
|
2,5x10-3
|
13,13
|
|
3x10-3
|
12,84
|
|
3,5x10-3
|
13,15
|
|
4x10-3
|
13,21
|
|
5x10-3
|
13,34
|
Tableau 4 : RMS des solutions de marées mondiales en fonction
des coefficients de frottement
Ces résultats montrent que la meilleure
RMS reste celle avec le coefficient de frottement 3x10-3. Cependant,
nous avons effectué la différence entre les solutions que
nous avons calculées (solutions avec 6 itérations et conditions
aux frontières ouvertes imposées, c’est-à-dire jusqu’à
l’étape 2 du calcul par CEFMO) et la solution CSR3.0. Une rapide
étude graphique des solutions obtenues comparée à
une des meilleures solutions de marée mondiale, semble montrer que
suivant les zones océaniques considérées ce coefficient
est plus ou moins bien adapté. Ainsi, par des études locales,
nous avons déterminé les meilleurs coefficients de frottement
pour nos 9 domaines océaniques :
-
3x10-3 pour le domaine ARCTIC ;
-
5x10-3 pour le domaine ATLNORD ;
-
5x10-3 pour le domaine ATLSUD ;
-
2x10-3 pour le domaine HUDSON ;
-
4x10-3 pour le domaine INDIEN ;
-
5x10-3 pour le domaine MALAYSIE ;
-
3x10-3 pour le domaine MEDITER ;
-
2x10-3 pour le domaine PACNORD ;
-
3x10-3 pour le domaine PACSUD.
Avec ces nouvelles valeurs nous avons assemblé
une nouvelle solution globale. Mais le calcul de la RMS obtenue avec la
base de données marégraphiques ST95 est de 13,40 cm. Cette
valeur est plus élevée que les RMS calculées avec
des coefficients de frottements constants sur toute la couverture océanique,
ce qui tend à prouver que la variation du coefficient sur un bassin
influe sur le calcul des solutions d’un autre bassin. Il faut donc comprendre
le mécanisme de dissipation de l’énergie afin de trouver
le bon coefficient de frottement sur chacun des bassins avant de pouvoir
fixer le frottement sur chaque bassin.
Nous avons donc utilisé un coefficient
de type Chézy égal à 3x10-3 pour toutes
nos simulations globales.
10.3 Assimilation de données
marégraphiques
10.3.1 Intérêts de l’assimilation
La plupart des modèles globaux de marées
disponibles à ce jour sont issus de l’analyse de données
altimétriques (T/P et ERS1/2). Ils ont apporté de grandes
améliorations en regard des modèles globaux de marées
plus anciens et ont atteint des précisions de l’ordre du centimètre
en plein océan [Shum et al., 1997]. Cependant des différences
plus importantes sont constatées en petits fonds (plateaux continentaux
et zones côtières) à cause de la complexité
et des caractéristiques spécifiques des ondes de marées
dans ces zones. Les longueurs d’onde sont plus courtes et les amplifications
régionales, souvent dues aux résonances locales, conduisent
à de forts gradients qui sont difficilement modélisables
par les modèles cités précédemment. De plus
des effets non-linéaires prennent place dans ces zones, ce qui génère
un spectre de marée beaucoup plus complexe que dans le plein océan.
Les analyses des données satellites
sont précises en plein océan, ce qui explique la grande qualité
des modèles globaux récents. Cependant près des côtes,
ces analyses ne peuvent pas être aussi précises du fait de
problèmes techniques lors de la mesure. En effet, des corrections
à faire ne sont plus aussi bonnes en zones côtières
telles les corrections ionosphériques et troposphériques
qui nécessitent une mesure par le radiomètre de T/P à
une distance d’au moins une trentaine de kilomètres des côtes.
D’autre part, les marégraphes sont
peu présents en plein océan (quelques marégraphes
plongeurs dans les eaux profondes), mais ils sont très nombreux
le long des côtes. En outre, les mesures marégraphiques sont
très précises du fait de leur courte période d’échantillonnage
(en général une heure) et de la qualité de la méthode
d’analyse harmonique utilisée. Ainsi, les marégraphes fournissent
une information précise du phénomène de marée
qui prend place en eaux peu profondes comparés aux données
de marées extraites de l’altimétrie. En effet, la qualité
de ces dernières est limitée par les problèmes d’aliasing
et de résolution spatiale dans ces zones.
Ainsi, notre but a été d’utiliser
cette information apportée par les mesures marégraphiques
grâce à notre méthode d’assimilation, pour calculer
de nouvelles solutions éléments finis de marée (FES98).
Ces solutions sont globales, améliorées le long des côtes
et sur les plateaux et indépendantes de l’altimétrie.
10.3.2 Schéma de l’assimilation
Comme nous l’avons mentionné ci-dessus,
les solutions libres manquent de précision. L’utilisation d’une
méthode d’assimilation de données marégraphiques qui
tient compte des informations apportées par la mesure de terrain,
va nous permettre de réduire les erreurs constatées entre
ces solutions libres et des données in situ. La méthode d’assimilation
a été présentée dans le Chapitre 9. Rappelons
juste qu’un représenteur est calculé pour chacun point de
mesure qui doit être assimilé. Il est représentatif
d’une perturbation instantanée à l’endroit de la donnée
assimilée, cette perturbation se propageant parmi l’océan
mondial dont la surface est modélisé de manière discrète
par la grille éléments finis. C’est pourquoi l’information
hydrodynamique de la marée est conservée car elle est intrinsèquement
contenue dans le représenteur. Les dimensions de chaque représenteur
sont celles du champs de dénivellation de la marée. La solution
assimilée complète est égale à la somme de
la solution libre plus une combinaison linéaire de représenteurs
pondérés par une valeur (poids) significative. Les poids
sont déterminés par les confiances qui sont allouées
à chaque donnée assimilée et par la minimisation d’une
fonction coût.
10.3.3 Données marégraphiques
assimilées
10.3.3.1 Sélection des banques
de données marégraphiques
L’utilisation de données marégraphiques
est un des buts principaux de notre travail, afin d’améliorer la
modélisation de la marée dans les eaux peu profondes tout
en restant indépendant de l’altimétrie. Le paragraphe 7.3
a introduit trois banques de données marégraphiques : WOCE,
IAPSO, BHI. Nous avons sélectionné nos données à
assimiler parmi ces banques. Un gros effort pour filtrer les bonnes données
des mauvaises a été entrepris (en particulier pour la banque
BHI). En effet, jusqu’à notre étude, aucun travail à
notre connaissance n’avait été entrepris pour sélectionner
des données marégraphiques à l’échelle mondiale
dans un but d’amélioration de solutions de marée grâce
à une technique d’assimilation.
Nous avons scindé notre sélection
en deux parties. Une partie des marégraphes est réservée
pour effectuer des comparaisons (ils proviennent des banques ST95 et ST727).
L’autre partie est utilisée pour l’assimilation. Cependant dans
certaines zones, il y a tellement peu de données marégraphiques,
que nous avons estimé nécessaire d’utiliser ces données
à la fois pour les comparaisons et l’assimilation. C’est pourquoi,
nous mettrons en place une banque de données altimétriques
indépendante de ces données marégraphique afin de
comparer nos solutions FES98. Ainsi, nous avons extrait de ces banques
de données une banque réduite pour chacune des huit ondes
calculées. Ces banques réduites ont été choisies
pour être représentatives de la physique des ondes de marées
à la fois en plein océan et le long des côtes. De même
que pour la construction de ST727, plusieurs critères ont été
appliqués pour sélectionner ces banques réduites à
partir des banques WOCE, IAPSO et BHI :
-
recherche des marégraphes à l’intérieur du maillage
global éléments finis ;
-
modification des coordonnées des marégraphes à 5 km
à l’extérieur des maillages pour qu’ils soient inclus dans
le maillage ;
-
étant donnée la qualité des données WOCE et
IAPSO, retrait de tous les marégraphes BHI qui sont à moins
de 20 km des marégraphes de ces deux premières banques ;
-
exclusion des marégraphes co-localisés ;
-
exclusion des marégraphes mesurant des phénomènes
locaux de résonance, d’étales ou d’effets non-linéaires
;
-
retrait des marégraphes dont la durée de mesure est inférieure
à 28 jours, car considérés comme fournissant une analyse
incomplète du spectre (problèmes de séparabilité
des ondes) ;
-
sélection des marégraphes BHI restants et qui n’ont pas plus
de 20% de différence en amplitude et 10° de phase avec les solutions
globales de marée CSR3.0 et FES94.1 ;
-
complément avec des marégraphes qui ne sont pas retenus par
les critères de sélections ci-dessus mais compatibles avec
des modèles locaux dans les Mers Arctiques [Lyard, 1997]
et les Mers de Chine [Lefèvre et al., 1999c] (une trentaine
de données).
Les critères appliqués ont surtout
permis de sélectionner les marégraphes de la banque BHI.
Ces critères ont été utilisé indépendamment
pour chaque onde. Au moyen de cette approche, nous avons retenu plusieurs
centaines de marégraphes pour chacune des ondes calculées
(cf. Tableau 17).
|
Onde
|
Nombre de données assimilées
|
|
M2
|
763
|
|
S2
|
733
|
|
N2
|
623
|
|
K2
|
636
|
|
2N2
|
232
|
|
K1
|
877
|
|
O1
|
881
|
|
Q1
|
634
|
Tableau 17 : Nombre de données assimilées suivant les
ondes pour obtenir FES98
Le nombre de marégraphes sélectionnés
varient suivant les ondes. En effet, les analyses harmoniques de la banque
BHI ont été faites par de nombreuses personnes depuis deux
siècles. Ces dernières ont utilisé des algorithmes
de calculs différents sur des séries temporelles de mesures
de qualité variable, ce qui ne permet d’obtenir le même nombre
d’ondes pour chacune des décompositions harmoniques de cette base.
La Figure 47 présente les cartes
de localisation des données marégraphiques assimilées
dans FES98 pour les huit ondes principales.
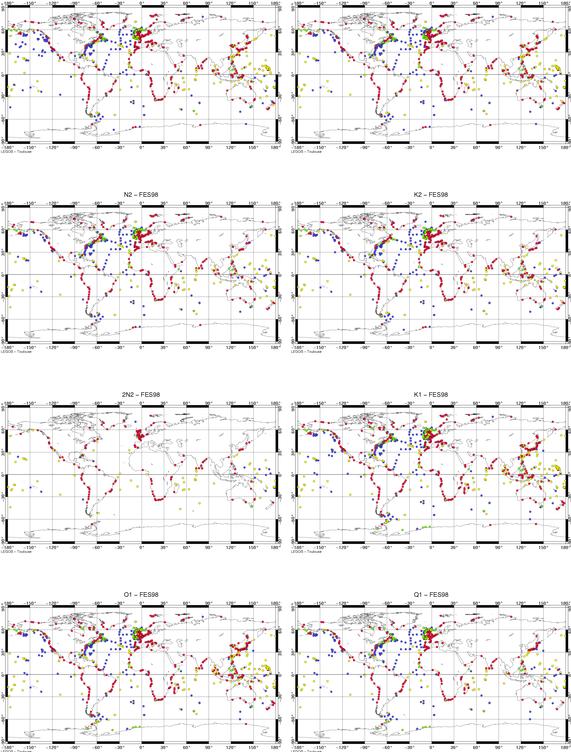
Figure 47 : Localisation des données
marégraphiques assimilées
10.3.3.2 Procédure d’assimilation
L’algorithme de calcul par les représenteurs
nécessite de donner une confiance (inverse de l’erreur) à
chacune des données assimilées et au modèle. Une grande
confiance sur une donnée va amplifier son influence sur la qualité
globale de la solution, alors qu’une faible confiance va localiser voire
lisser son effet. Donner une confiance sur chacune des données à
assimiler est une phase clé du schéma de l’assimilation.
Or, les marégraphes et plus particulièrement les analyses
des marégraphes, ne sont pas fournis avec des barres d’erreur qui
sont tout autant d’information sur la qualité de la mesure, des
erreurs instrumentales, des problèmes rencontrés au cours
de l’analyse harmonique. De nombreux phénomènes peuvent expliquer
ces erreurs. Nous avons donc eu recours à une méthode empirique
de détermination des erreurs sur les mesures marégraphiques.
Nous estimons que les données WOCE
et IAPSO sont de meilleures qualités que les données BHI
(de façon générale). Les techniques de mesures et
de décompositions harmoniques ne sont pas comparables. Ces données
peuvent être distinguées par leur localisation. En effet,
la banque IAPSO n’est composée que d’appareils de grand fond qui
ne mesurent donc pas les phénomènes côtiers de la marée.
Les analyses sont donc a priori meilleures. La plupart des données
WOCE proviennent du même type d’appareil et les méthodes d’analyse
pour en extraire les composantes de la marée sont robustes et bien
vérifiées. Ces données peuvent être considérées
comme fiable et de bonne qualité. Par contre les données
BHI sont côtières et d’origine très diverses, donc
de qualité variable. Ainsi, en classant les marégraphes suivant
leur situation par rapport au fond océanique, nous pouvons déterminer
empiriquement une confiance acceptable pour chacune des données.
Au moyen de la carte bathymétrique des fonds marins utilisées
dans la modélisation, nous avons classé les marégraphes
sélectionnés pour l’assimilation en 4 familles :
-
la zone côtière (petit fonds compris entre la surface et 100
m) ;
-
la zone de plateaux (fonds entre 100 m et 500 m) ;
-
la zone de plein océan (fonds inférieurs à 500 m)
;
-
la zone insulaire (comme la zone côtière mais fonds océaniques
à pente très forte, en bref , zone autour des îles).
Dans l’océan profond, les interactions
entre les ondes sont faibles et ce sont de bonnes mesures (IAPSO, WOCE)
qui permettent de déterminer les composantes de ces ondes de marée.
C’est pourquoi, nous avons donné une confiance de 0,25 cm aux données
de la zone de plein océan. Pour les zones côtières
et insulaires, ce n’est pas le cas. Les analyses sont supposées
être moins bonnes. Nous avons fixé leur confiance à
2,5 cm. Pour faire une transition entre les petits fonds et le plein océan,
nous avons donné une confiance de 1 cm aux données de plateaux.
Pour les données de la zone insulaire, après plusieurs essais
numériques, nous avons finalement fixé leur confiance à
2.5 cm. Ces confiances ont été attribuées après
concertations entre scientifiques ayant étudié et utilisés
les mesures marégraphiques. Pour rendre compte de ces différente
zones, nous donnons pour l’onde M2 la carte de répartition
des marégraphes Figure 48. Les points rouges représentent
les marégraphes côtiers, les verts, ceux de plateaux, les
jaunes, ceux près des îles, et les bleus, les marégraphes
de plein océan.
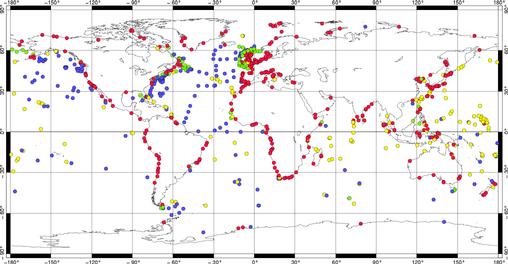
Figure 48 : Répartition des
zones de marégraphes pour l’attribution des confiances
Le Tableau 18 présente le nombre
de marégraphes assimilés par zone.
|
Onde
|
M2
|
S2
|
N2
|
K2
|
2N2
|
K1
|
O1
|
Q1
|
|
Côtiers
|
351
|
350
|
284
|
315
|
149
|
436
|
438
|
268
|
|
Plateaux
|
91
|
90
|
86
|
73
|
6
|
104
|
105
|
100
|
|
Iles
|
152
|
152
|
110
|
117
|
67
|
178
|
179
|
97
|
|
Pélagique
|
189
|
165
|
156
|
151
|
15
|
179
|
179
|
174
|
|
Total
|
783
|
757
|
636
|
656
|
237
|
897
|
901
|
639
|
Tableau 18 : Nombre de marégraphes par zone
Ce nombre de marégraphes est plus
important en zone côtière. C’est la conséquence du
nombre beaucoup plus élevé de ces appareils de mesure en
petit fonds. Cependant, le nombre de marégraphes en zone pélagique
est malgré tout assez important (un peu plus de 50% du nombre de
marégraphes côtiers en moyenne). La qualité des mesures
des marégraphes de pression de fond et la quasi-absence d’interactions
entre les ondes en plein océan font que les analyses harmoniques
des mesures de ces appareils sont bonnes, d’où leur importance dans
notre sélection.
En outre, dans le cadre de l’assimilation
de données, nous nous sommes placés en contrainte faible.
C’est-à-dire que nous considérons que notre modèle
n’est pas parfait. En effet, les équations ne sont pas exactement
le reflet de la réalité, nous avons fait de nombreuses approximations
et les problèmes numériques au cours de la résolution
des équation par CEFMO ne sont pas inexistants. C’est pourquoi,
nous imposons aussi une erreur sur le modèle. Comme nous ne pouvons
pas quantifier directement cette erreur sur le modèle, nous l’estimons
par le biais d’une erreur sur le forçage, en considérant
que ce dernier à une variance uniforme et une covariance spatiale
qui à la forme d’une gaussienne.
10.4 Qualité des solutions
Ainsi, la nouvelle formulation du modèle
hydrodynamique nous a permis de calculer de nouvelles solutions à
l’échelle globale. Grâce à la résolution par
blocs, ces nouvelles solutions sont purement hydrodynamiques car elles
ne sont forcées que par le potentiel astronomique et les effets
de charges et d’auto-attraction. Les huit ondes M2, S2,
N2,
K2,
2N2, K2,
O1 et Q1
sont donc calculées sous formes de solutions libres, affranchies
des perturbations des conditions aux limites initiales imposées
aux frontières ouvertes afin de permettre une convergence rapide
des solutions.
Afin d’évaluer la qualité
des nouvelles solutions FES98, nous avons effectué plusieurs comparaisons
avec les autres modèles FES (FES94.1 et FES95.2.1). FES95.2.1 est
une version réduites de FES95.2 :quelques zones littorales affectées
par de gros problèmes de résonance ont été
retirées. La qualité de la solution en est bien sur améliorée,
mais, surtout, sa qualité en plein océan n’est pas occultée
par les quelques zones côtières détériorées.
Nous avons effectué les comparaisons
avec trois banques de données :
-
la banque de données marégraphiques pélagiques ST95
;
-
la banque de données marégraphiques côtières
ST727 ;
-
une banque de données altimétriques Topex.
10.4.1.1 Comparaisons aux données
marégraphiques pélagiques
La comparaison des solutions FES avec ST95
nous permet d’évaluer leur qualité en plein océan
par rapport à la marégraphie. Le Tableau 19 illustre les
améliorations sensibles que FES98 apporte pour toutes les ondes
principales, excepté pour 2N2 pour laquelle beaucoup
moins de données ont été assimilées. La précision
atteint maintenant 1,5 cm pour une RSS de 2,41 cm. Il faut cependant noter
qu’étant donné la qualité des données de la
banque ST95, nous retrouvons quelques-unes unes de ces données de
comparaison dans les données que nous avons assimilées. Ainsi
58 données de ST95 ont été assimilées pour
obtenir FES98. C’est pourquoi, pour plus de fiabilité dans notre
validation, nous avons comparé FES98 à d’autres banques de
données.
|
Onde
|
RMS sur les données (cm)
|
Nombre de données
|
FES94.1
RMS (cm)
|
FES95.2.1
RMS (cm)
|
FES98
RMS (cm)
|
|
M2
|
33,55
|
95
|
2,85
|
1,74
|
1,51
|
|
S2
|
12,81
|
95
|
1,57
|
1,12
|
0,86
|
|
N2
|
6,79
|
91
|
0,91
|
0,89
|
0,80
|
|
K2
|
3,32
|
90
|
0,48
|
0,48
|
0,35
|
|
2N2
|
1,01
|
90
|
0,29
|
0,29
|
0,31
|
|
K1
|
11,10
|
95
|
1,19
|
1,17
|
1,00
|
|
O1
|
7,66
|
95
|
1,09
|
1,05
|
0,93
|
|
Q1
|
1,61
|
87
|
0,28
|
0,28
|
0,25
|
|
RSS
|
-
|
-
|
3,80
|
2,82
|
2,41
|
Tableau 19 : Comparaisons numériques pour ST95
10.4.1.2 Comparaisons aux données
côtières
L’amélioration des solutions hydrodynamiques
globales était un des objectifs à atteindre en produisant
FES98. C’est pourquoi, de nombreuses données marégraphiques
de qualité ont été assimilées en milieu côtier.
Mais qu’en est-il de la qualité des solutions obtenues dans ces
zones ? La banque ST727 nous offre un outil de comparaison intéressant
pour l’évaluer (cf. Tableau 20), car elle est représentative
des phénomènes locaux de marée le long des principales
côtes de l’océan mondial. Les améliorations y sont
importantes. Les comparaisons peuvent être considérées
comme fiables car seulement 53 données de ST727 ont été
assimilées dans FES98. En particulier, en comparant FES98 à
la solution altimétrique FES95.2.1, ces améliorations sont
d’un facteur 2. La RSS de FES98 le long des côtes est de 14,40 cm
soit 4,03 cm de moins que FES94.1. Nous pouvons donc estimer que FES98
(en RSS par rapport à ST727) est 22% plus précise que FES94.1
jusqu’à présent considérée par la communauté
scientifique comme étant la meilleure solution hydrodynamique en
milieu côtier.
|
Onde
|
RMS sur les données (cm)
|
Nombre de données
|
FES94.1
RMS (cm)
|
FES95.2.1
RMS (cm)
|
FES98
RMS (cm)
|
|
M2
|
57,78
|
727
|
14,69
|
22,02
|
10,99
|
|
S2
|
22,04
|
725
|
6,84
|
18,82
|
5,56
|
|
N2
|
12,18
|
617
|
4,32
|
5,12
|
3,66
|
|
K2
|
6,54
|
616
|
2,54
|
2,54
|
2,24
|
|
2N2
|
1,84
|
263
|
1,18
|
1,18
|
1,09
|
|
K1
|
13,48
|
724
|
5,50
|
7,08
|
4,71
|
|
O1
|
9,74
|
720
|
4,37
|
4,54
|
3,56
|
|
Q1
|
2,01
|
402
|
1,09
|
1,08
|
1,11
|
|
RSS
|
-
|
-
|
18,43
|
30,74
|
14,40
|
Tableau 20 : Comparaisons numériques pour ST727
10.4.1.3 Comparaisons à l’altimétrie
Cependant, afin d’affiner encore plus les
comparaisons, nous avons voulu comparer nos solutions par rapport à
une troisième source de données indépendantes de la
marégraphie. C’est pourquoi nous avons comparé nos solutions
FES à une banque de données altimétriques issues de
points de croisement T/P (Schrama, communication personnelle, 1999).
Cette banque nous donne accès à l’analyse harmonique de la
marée en plus de 5000 points pour les ondes de marée M2,
S2,
K2,
N2,
K1,
O1,
P1,et
Q1.
Les comparaisons montrent que FES95.2.1 est la meilleure solution comparée
à cette banque (cf. Tableau 21), ce qui est a priori normal puisque
cette solution FES a été obtenue en assimilant des données
altimétriques T/P. Par contre, nous pouvons constater une amélioration
certaine de FES98 par rapport à FES94.1 : 25% pour M2
et 11% pour K1.
|
Onde
|
RMS sur les données (cm)
|
Nombre de données
|
FES94.1
RMS (cm)
|
FES95.2.1
RMS (cm)
|
FES98
RMS (cm)
|
|
M2
|
25,85
|
5313
|
3,32
|
1,33
|
2,51
|
|
S2
|
9,71
|
5313
|
1,62
|
0,82
|
1,19
|
|
N2
|
5,59
|
5313
|
1,01
|
0,75
|
0,82
|
|
K2
|
2,83
|
5313
|
0,99
|
0,97
|
0,98
|
|
2N2
|
-
|
-
|
-
|
-
|
-
|
|
K1
|
10,00
|
5313
|
1,80
|
1,11
|
1,61
|
|
O1
|
7,20
|
5313
|
1,11
|
0,87
|
1,14
|
|
Q1
|
1,70
|
5313
|
1,61
|
0,83
|
0,83
|
|
RSS
|
-
|
-
|
4,72
|
2,57
|
3,73
|
Tableau 21 : Comparaisons numériques pour la banque Topex
10.5 Extension du spectre de marée
10.5.1 Décomposition du spectre
Dans le Chapitre 7, nous avons donné
des décompositions de spectre basées sur les deux banques
de données marégraphiques (ST95 et ST727). Ces deux décompositions
sont représentatives de l’importance des différentes ondes
du spectre à l’échelle globale, que ce soit en plein océan
(ST95) ou le long des côtes (ST727). La Figure 16 illustre l’importance
des différentes ondes dans la décomposition du spectre de
marée. Nous avons calculé le pourcentage de RMS de chaque
onde par rapport à la RMS globale.
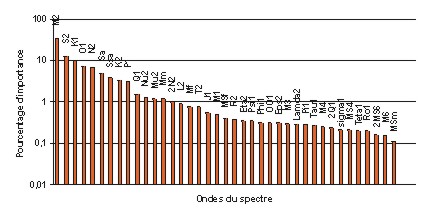
Figure 49 : Importance des ondes dans
la décomposition harmonique du spectre de marée pour ST95
Le Tableau 22 donne les importances en
pourcentage des 8 ondes calculées.
|
Onde
|
Pourcentage d’importance
|
|
M2
|
33,5%
|
|
S2
|
12,6%
|
|
K1
|
10,1%
|
|
O1
|
7,0%
|
|
N2
|
6,8%
|
|
K2
|
3,3%
|
|
Q1
|
1,5%
|
|
2N2
|
1,0%
|
|
Total
|
75,9%
|
Tableau 22 : Pourcentage d’importance des principales ondes du spectre
Ainsi, les 8 ondes calculées ne
représentent que 75,9% du spectre total de la marée déduit
des 95 données marégraphiques de la banque ST95. La décomposition
harmonique de ST95 montre que même en plein océan, les 8 ondes
principales ne suffisent pas à expliquer tout le spectre. En effet,
outre les ondes longues périodes Sa, Ssa,
et Mm il existe 4 autres ondes (P1,
n2,
m2
et L2) dont l’amplitude est de plus de 1 centimètre
et qui représente chacune plus de 1% du spectre.
Il apparaît donc clairement que compléter
le spectre de marée est essentiel si nous voulons accroître
la précision de la prédiction.
10.5.2 Ondes secondaires
10.5.2.1 Méthode d’admittance
Afin d’augmenter le nombre de composantes
du spectre de marée il est possible de calculer de nouvelles ondes
sans avoir recours à un nouveau modèle de marée identique
à celui qui a permis d’obtenir les 8 ondes principales. Cette méthode
repose sur le principe d’admittance qui s’appuie sur la méthode
harmonique.
La méthode harmonique est basée
sur un développement quasi périodique en temps du potentiel
de marée donné par Doodson [1921]. Comme l’a montrée
le Chapitre 4, il est composé de plus de 400 composantes. D’habitude,
pour des prédictions de marées océaniques, un spectre
simplifié est utilisé : seules les composantes majeures sont
conservées. Des facteurs de corrections nodales, variant très
lentement sur la période chaldéenne (18,61 années),
sont alors introduits pour corriger ce spectre réduit.
10.5.2.2 L’approche par admittance
Une façon d’accorder les composantes
secondaires aux composantes principales qui leurs sont voisines dans le
spectre est de relier la réponse régulière de l’océan
au potentiel astronomique. D’après Munk et Cartwright [1966],
l’admittance est le rapport de l’onde de marée observée et
de sa marée d’équilibre au méridien de Greenwich.
Elle est donc dépendante de la fréquence de l’onde considérée.
En reprenant les notations introduites par Le Provost et al. [1991],
pour une composante de marée d’indice m, l’admittance est
définie par :

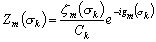 (10.129)
(10.129)
avec :
-
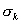 la fréquence de la composante
de marée d’indice k ;
la fréquence de la composante
de marée d’indice k ;
-
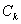 l’amplitude de la marée d’équilibre
de la composante k ;
l’amplitude de la marée d’équilibre
de la composante k ;
-
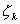 l’amplitude de la composante d’indice
k ;
l’amplitude de la composante d’indice
k ;
-
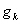 la phase de la composante d’indice
k référencée par rapport au méridien de Greenwich.
la phase de la composante d’indice
k référencée par rapport au méridien de Greenwich.
Une façon d’obtenir ces fonctions d’admittance
est d’utiliser la méthode harmonique classique et de définir
des approximations analytiques parmi chacune des espèces diurnes
et semi-diurnes.
10.5.2.3 Rappels sur la marée
d’équilibre
Le calcul par admittance introduit la notion
de marée d’équilibre définit comme étant la
forme hypothétique globale qu’aurait la surface des océans
si elle était en équilibre avec les forces engendrées
par le potentiel générateur, en l’absence de toute inertie
et de courants. Elle est communément approchée par le potentiel
générateur multiplié par le rapport 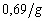 .
Cependant des modifications sont à appliquer si le contour des continents
et des océans est pris en compte.
.
Cependant des modifications sont à appliquer si le contour des continents
et des océans est pris en compte.
La marée d’équilibre dérive
du potentiel générateur (cf. paragraphe 4.2.3). Elle ne dépend
que de la position du point considéré sur la surface des
océans et de la classe de l’onde (semi-diurne, diurne, longue période).
Pour un point de coordonnées 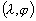 la marée d’équilibre (amplitude a, phase p)
sera le coefficient d’équilibre donné par les tables de Doodson
[1921] pour l’onde considérée, multiplié par un coefficient
d’amplitude a et de phase p donnés par :
la marée d’équilibre (amplitude a, phase p)
sera le coefficient d’équilibre donné par les tables de Doodson
[1921] pour l’onde considérée, multiplié par un coefficient
d’amplitude a et de phase p donnés par :
-
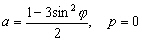 pour les ondes longues périodes
(classe 0) ;
pour les ondes longues périodes
(classe 0) ;
-
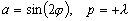 pour les ondes diurnes (classe 1)
;
pour les ondes diurnes (classe 1)
;
-
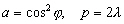 pour les ondes semi-diurne (classe
2).
pour les ondes semi-diurne (classe
2).
Les longitudes sont référencées
par rapport au méridien de Greenwich.
10.5.2.4 Fonctions splines
Ainsi pour obtenir le coefficient d’admittance
d’une onde secondaire, il suffit de faire une interpolation (voire une
extrapolation) avec deux des coefficients d’admittance des ondes principales
qui lui sont voisines (du point de vue de la période des ondes).
Cependant, une régression linéaire
peut être trop grossière pour décrire la courbe d’admittance
de certaines ondes secondaires dans certaines zones de l’océan global.
C’est pourquoi des fonctions splines cubiques utilisant les caractéristiques
de trois ondes de marée permettent de pallier ce problème.
Cartwrigth
et al. [1988] furent les premiers à introduire ces fonctions
sous la forme :

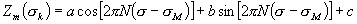 (10.130)
(10.130)
avec :
-
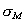 la fréquence de l’onde M2
;
la fréquence de l’onde M2
;
-
a, b et c les coefficients complexes ajustés
aux ondes principales M2, N2, K2.
Avec ces splines, la forme de la courbe d’admittance
peut-être mieux ajustée.
En négligeant les effets radiationnels
et non linéaires, les ondes 2N2, n2,
m2,
L2
et T2 peuvent être déduites par admittance.
Le même raisonnement peut-être
appliqué à l’espèce diurne.
10.5.2.5 Calcul des ondes secondaires
Grâce aux calculs des solutions globales
des 8 ondes principales (M2, S2, N2,
K2,
2N2 pour les semi-diurnes et K1,
O1,
et Q1 pour les diurnes) et l’utilisation de la méthode
d’admittance décrite au paragraphe 10.5.2.2 nous pouvons compléter
le spectre de marée de FES98 avec des ondes secondaires. L’importance
de ces ondes secondaires a été déterminée par
des décompositions harmoniques de mesures marégraphiques.
Ainsi, 19 ondes ont été calculées pour tous les points
du maillage global éléments finis :
-
m2, n2, L2, l2
et T2 calculées à partir de splines sur
les ondes M2, N2 et K2 ;
-
e 2 calculée à partir d’une interpolation
linéaire sur 2N2 et N2 ;
-
h 2 calculée à partir d’une interpolation
linéaire sur M2 et K2 ;
-
P1 calculée à partir de splines sur les
ondes Q1, O1 et K1 ;
-
2Q1, r1, s1 calculées
à partir d’interpolations linéaires sur Q1
et O1 ;
-
J1, c1, M11, M12,
OO1,
j1, p1, et q1 calculées
à partir d’interpolations linéaires sur
O1
et K1.
Le spectre de marée de FES98 devient
ainsi beaucoup plus complet.
10.5.3 Ondes longues périodes
Pour affiner encore plus le spectre de FES98,
nous avons ajouté aux ondes principales et secondaires, trois ondes
longues périodes déterminées par Lyard [1998]
: Mf, Mm, et Mtm.
Les ondes Mf et Mm ont été
calculées par la méthode d’assimilation. L’onde Mtm
est hydrodynamique.
10.6 Bilan sur FES98
Nous avons mis en place une nouvelle version
de notre modèle hydrodynamique éléments finis combiné
à une procédure d’assimilation. Les améliorations
apportées par la résolution par blocs ont permis de calculer
des solutions de marées à l’échelle globale affranchies
de conditions imposées aux frontières ouvertes des sous domaines
du maillage. Ces solutions libres, uniquement forcées par le potentiel
astronomique et les effets secondaires d’auto-attraction et d’effets de
charge, ont été calculées pour M2,
S2,
N2,
K2,
2N2,
K1,
O1 et Q1.
La méthode d’assimilation qui avait été utilisée
pour FES95.2.1 a été revue et corrigée afin de ne
plus avoir d’effets de résonance anormaux en quelques zones côtières.
Pour chacune des huit ondes, une banque de plusieurs centaines de données
réparties sur l’océan mondial et majoritairement le long
des côtes, a été constituée. Ces données
ont été soigneusement extraites des banques WOCE, IAPSO et
BHI et ont été assimilées dans les solutions libres.
Ces nouvelles solutions indépendantes de la mesure altimétrique
ont été comparées à la marégraphie et
l’altimétrie et montrent de réelles améliorations
en particulier en zones côtières. Afin de compléter
le spectre de marée 19 autres composantes ont été
déduites par admittance : m2,
n2,
L2,
l2,T2,
e2,
h2,
P1,
2Q1,
r1,
s1,
J1, c1,
M11,
M12,
OO1,
j1,
p1,
et q1.
De plus, 3 ondes longues périodes ont été ajoutées
: Mf, Mm et Mtm.
Ces nouvelles solutions éléments
finis ont été projetées sur des grilles régulières
et sont disponibles sur des grilles de 0,25°x0,25°.
Cependant comme nous l’avons vu dans les
comparaisons, l’amélioration est très sensible en zone côtière
et nettement moins en zone pélagique. En effet, la principale source
d’amélioration est donnée par l’assimilation de marégraphes
placés le long des côtes. Il nous manque donc de l’information
en plein océan.
Back |
Next
Title: Thèse de Fabien Lefèvre
Issue: Version 1.0
Date: 29/09/2000


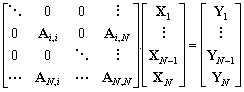 (10.110)
(10.110)
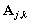 : les matrices de coefficients fixés
par les équations hydrodynamiques et imposant les dépendances
entre les nœuds du maillage ;
: les matrices de coefficients fixés
par les équations hydrodynamiques et imposant les dépendances
entre les nœuds du maillage ;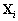 : les vecteurs d’inconnues strictement
à l’intérieur du bassin i ;
: les vecteurs d’inconnues strictement
à l’intérieur du bassin i ;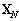 : le vecteur d’inconnues partagées
entre deux bassins (pour tous les N-1 bassins) ;
: le vecteur d’inconnues partagées
entre deux bassins (pour tous les N-1 bassins) ;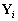 : le forçage total appliqué
sur le bassin océanique i ;
: le forçage total appliqué
sur le bassin océanique i ;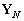 : le forçage total appliqué
sur les frontières ouvertes partagées.
: le forçage total appliqué
sur les frontières ouvertes partagées.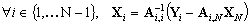 (10.111)
(10.111)
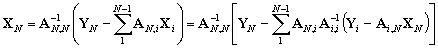 (10.112)
(10.112)
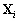 sous la forme :
sous la forme :
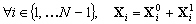 (10.113)
(10.113)
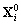 : les vecteurs d’inconnues strictement
à l’intérieur du bassin i et qui ne sont que la conséquence
du forçage naturel ;
: les vecteurs d’inconnues strictement
à l’intérieur du bassin i et qui ne sont que la conséquence
du forçage naturel ;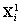 : les vecteurs d’inconnues strictement
à l’intérieur du bassin i et qui ne sont que la conséquence
du forçage imposé par nos conditions aux limites ;
: les vecteurs d’inconnues strictement
à l’intérieur du bassin i et qui ne sont que la conséquence
du forçage imposé par nos conditions aux limites ;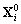 car ils sont exempts
de l’influence des conditions aux limites qui nous permettent a priori
d’assurer le calcul des solutions de marées sur chaque sous domaine
et la continuité entre les sous domaines du maillage de l’océan
mondial.
car ils sont exempts
de l’influence des conditions aux limites qui nous permettent a priori
d’assurer le calcul des solutions de marées sur chaque sous domaine
et la continuité entre les sous domaines du maillage de l’océan
mondial.
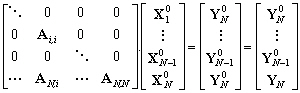 (10.114)
(10.114)
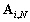 puisque les conditions aux
limites sont nulles dans le calcul des
puisque les conditions aux
limites sont nulles dans le calcul des 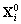 .
Nous ne considérons que la part du forçage astronomique.
Nous en déduisons :
.
Nous ne considérons que la part du forçage astronomique.
Nous en déduisons :
 (10.115)
(10.115)
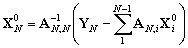 (10.116)
(10.116)
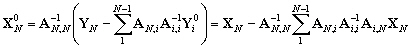 (10.117)
(10.117)
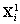 peuvent être considérés comme des perturbations de
la solution libre. En effet, ils représentent la contribution dans
la solution forcée des conditions aux limites forcées, sans
influence du potentiel naturel. Ainsi, d’après (10.110) le système
qui est l’unique conséquence des conditions aux limites imposées
s’écrit :
peuvent être considérés comme des perturbations de
la solution libre. En effet, ils représentent la contribution dans
la solution forcée des conditions aux limites forcées, sans
influence du potentiel naturel. Ainsi, d’après (10.110) le système
qui est l’unique conséquence des conditions aux limites imposées
s’écrit :
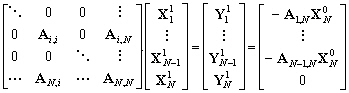 (10.118)
(10.118)
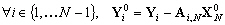 (10.119)
(10.119)
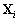 de
(10.112). En reportant, les valeurs des vecteurs
de
(10.112). En reportant, les valeurs des vecteurs  données par (10.111) dans (10.112) pour tous les indices i
variant de 1 à N1, nous obtenons après simplifications
:
données par (10.111) dans (10.112) pour tous les indices i
variant de 1 à N1, nous obtenons après simplifications
:
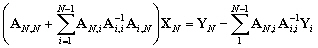 (10.120)
(10.120)
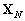 .
Le problème ici est que cette résolution implique le calcul
de l’inverse de la matrice globale
.
Le problème ici est que cette résolution implique le calcul
de l’inverse de la matrice globale 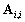 ce qui est impossible étant donnée la taille de cette matrice.
Le calcul direct est donc compromis. Il faudrait utiliser une résolution
itérative, lourde et coûteuse pour résoudre (10.120).
ce qui est impossible étant donnée la taille de cette matrice.
Le calcul direct est donc compromis. Il faudrait utiliser une résolution
itérative, lourde et coûteuse pour résoudre (10.120).
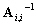 est multipliée
par des matrices
est multipliée
par des matrices 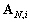 et
et 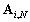 telles que tous les coefficients de la matrice inverse ne sont pas nécessaires.
En effet, les matrices
telles que tous les coefficients de la matrice inverse ne sont pas nécessaires.
En effet, les matrices 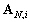 et
et 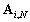 ne contiennent que des coefficients d’équations ne faisant intervenir
que les nœuds frontières et les nœuds auxquels ils sont connectés,
c’est-à-dire les nœuds voisins de ces nœuds frontières. Les
inconnues strictement intérieures d’un bassin i peuvent être
séparées en deux groupes :
ne contiennent que des coefficients d’équations ne faisant intervenir
que les nœuds frontières et les nœuds auxquels ils sont connectés,
c’est-à-dire les nœuds voisins de ces nœuds frontières. Les
inconnues strictement intérieures d’un bassin i peuvent être
séparées en deux groupes :
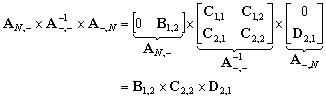 (10.121)
(10.121)
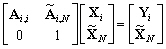 (10.122)
(10.122)
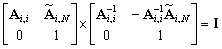 (10.123)
(10.123)
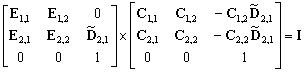 (10.124)
(10.124)
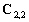 est
dimensionné par le carré du nombre de nœuds qui sont voisins
d’au moins un nœud partagé sur une frontière ouverte. Ce
terme peut être calculé par les matrices inverses déduites
du problème a priori (méthode de réponse impulsionnelle)
sur chacun des bassins.
est
dimensionné par le carré du nombre de nœuds qui sont voisins
d’au moins un nœud partagé sur une frontière ouverte. Ce
terme peut être calculé par les matrices inverses déduites
du problème a priori (méthode de réponse impulsionnelle)
sur chacun des bassins.
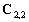 , nous en déduisons
les termes
, nous en déduisons
les termes 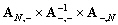 . Puis nous pouvons
calculer
. Puis nous pouvons
calculer 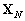 à partir de
(10.120). Une fois que nous avons calculé le vecteur
à partir de
(10.120). Une fois que nous avons calculé le vecteur 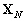 ,
nous pouvons le reporter dans (10.117), ce qui nous donne le vecteur
,
nous pouvons le reporter dans (10.117), ce qui nous donne le vecteur 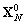 .
De là nous en déduisons les vecteurs
.
De là nous en déduisons les vecteurs 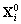 .
Nous avons ainsi résolu le problème de détermination
des inconnues aux frontières ouvertes.
.
Nous avons ainsi résolu le problème de détermination
des inconnues aux frontières ouvertes.
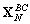 aux
frontières ouvertes, alors la solution vectorielle des nœuds partagés
est donnée par :
aux
frontières ouvertes, alors la solution vectorielle des nœuds partagés
est donnée par :
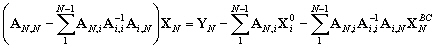 (10.125)
(10.125)
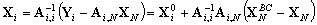 (10.126)
(10.126)
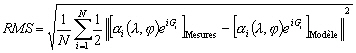 (10.127)
(10.127)
 la norme telle que pour un complexe
:
la norme telle que pour un complexe
: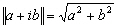 ;
;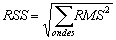 (10.128)
(10.128)





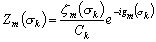 (10.129)
(10.129)
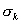 la fréquence de la composante
de marée d’indice k ;
la fréquence de la composante
de marée d’indice k ;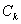 l’amplitude de la marée d’équilibre
de la composante k ;
l’amplitude de la marée d’équilibre
de la composante k ;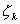 l’amplitude de la composante d’indice
k ;
l’amplitude de la composante d’indice
k ;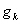 la phase de la composante d’indice
k référencée par rapport au méridien de Greenwich.
la phase de la composante d’indice
k référencée par rapport au méridien de Greenwich.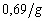 .
Cependant des modifications sont à appliquer si le contour des continents
et des océans est pris en compte.
.
Cependant des modifications sont à appliquer si le contour des continents
et des océans est pris en compte.
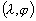 la marée d’équilibre (amplitude a, phase p)
sera le coefficient d’équilibre donné par les tables de Doodson
[1921] pour l’onde considérée, multiplié par un coefficient
d’amplitude a et de phase p donnés par :
la marée d’équilibre (amplitude a, phase p)
sera le coefficient d’équilibre donné par les tables de Doodson
[1921] pour l’onde considérée, multiplié par un coefficient
d’amplitude a et de phase p donnés par :
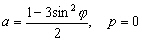 pour les ondes longues périodes
(classe 0) ;
pour les ondes longues périodes
(classe 0) ;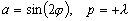 pour les ondes diurnes (classe 1)
;
pour les ondes diurnes (classe 1)
;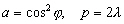 pour les ondes semi-diurne (classe
2).
pour les ondes semi-diurne (classe
2).
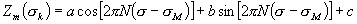 (10.130)
(10.130)
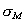 la fréquence de l’onde M2
;
la fréquence de l’onde M2
;