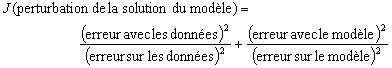Chapitre 11 FES99 : un modèle global issu de
la marégraphie et de l’altimétrie
11.1 Présentation du chapitre
Le calcul des solutions de marée hydrodynamique
utilisant la technique d’assimilation basée sur la méthode
des représenteurs nous a permis d’obtenir les solutions globales
de marée FES98. D’après les comparaisons faites dans le chapitre
précédent, FES98 a apporté une bonne amélioration
des solutions FES en milieu côtier. Même si sa qualité
est bonne en plein océan, celle-ci n’est pas suffisante pour les
applications liées à l’altimétrie. Nous avons donc
souhaité produire un nouveau jeu de solutions FES qui, grâce
à l’expertise que nous avons acquise en construisant FES98, vont
être de bonne précision le long des côtes et en plein
océan. C’est pourquoi nous allons interpréter les représenteurs
afin de mieux en appréhender les effets sur le calcul d’une solution
globale. Puis, pour affiner la précision des solutions, nous assimilerons
des données issues de l’analyse altimétrique en plein océan.
Ces analyses ont été réalisées au cours d’une
collaboration avec E.J.O. Schrama du DEOS (Delft institute for Earth Oriented
Space research) au Pays-Bas. Cette approche nous permet de produire les
solutions éléments finis FES99 qui sont, à la base,
hydrodynamiques et perfectionnées par l’assimilation de données
marégraphiques et altimétriques.
11.2 Interprétation de l’assimilation
11.2.1 Rappels
Pour le calcul de FES98, nous n’avions pas
de solution modélisée de marée pouvant nous donner
matière à interpréter réellement les effets
de l’assimilation de données marégraphiques par la méthode
des représenteurs dans notre modèle hydrodynamique. Dans
la perspective du calcul de nouvelles solutions assimilées, nous
avons cherché à qualifier les apports de l’assimilation en
interprétant les représenteurs qui lui sont associés.
Le Chapitre 9 a introduit cette notion
de représenteurs rk par l’introduction d’un produit
scalaire :
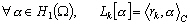 (11.131)
(11.131)
avec :
-
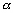 : le champ de dénivellation
(de dimension le nombre de nœuds du maillage) ;
: le champ de dénivellation
(de dimension le nombre de nœuds du maillage) ;
-
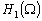 : l’espace des dénivellations
;
: l’espace des dénivellations
;
-
 : la fonctionnelle linéaire
qui au champ
: la fonctionnelle linéaire
qui au champ 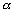 associe la dénivellation
au point de la donnée assimilée k ;
associe la dénivellation
au point de la donnée assimilée k ;
-
 : le produit scalaire prenant en
compte les erreurs sur le modèle.
: le produit scalaire prenant en
compte les erreurs sur le modèle.
11.2.2 Aspects géométriques
des représenteurs
Dans notre approche de l’assimilation, la
forme analytique des représenteurs n’est pas simple. L’étude
de plus d’une centaine de représenteurs associés aux données
marégraphiques que nous avons assimilé dans FES98, nous a
permis d’en extraire les principales caractéristiques. Pour les
illustrer, nous avons choisi et tracé trois représenteurs
calculés au cours de la construction de FES98 pour l’onde M2.
Ces représenteurs sont associés aux données de trois
stations marégraphiques situées dans des zones de fonds différents
:
-
les données marégraphiques de la station côtière
de Port Tudy sur les côtes bretonnes françaises ;
-
les données du marégraphe plongeur IAPSO 1.4.32 mouillé
sur un fond d’environ 970 m dans l’océan Atlantique Sud ;
-
les données marégraphiques de la station de l’île de
Saint Paul dans l’océan Indien.
Nous avons tracé les amplitudes normalisées
des représenteurs, c’est-à-dire que nous avons divisé
les amplitudes en chaque point du champ du représenteur par l’amplitude
de la donnée marégraphique associée. Ainsi, nous avons
une valeur de 1 au niveau du marégraphe pour les trois représentation
sur carte. Une valeur inférieure (respectivement supérieure)
à 1 indique que le représenteur propagera peu (respectivement
de manière importante) l’information introduite par l’assimilation
de sa donnée marégraphique. De plus, nous avons tracé
les phases de ces représenteurs qui sont référencées
entre 0 et 360°. Sur les six figures qui suivent, le point clair indique
la position du marégraphe auquel est associé le représenteur.
11.2.2.1 Représenteur en zone
côtière
Le représenteur associé à
la donnée de Port Tudy présente une petite zone autour du
marégraphe (point jaune) où l’amplitude est importante, particulièrement
dans la Manche et de façon moindre sur le plateau Européen
et la Mer du Nord (Figure 50). Ailleurs, dans le reste de l’océan
mondial, les amplitudes normalisées sont toutes inférieures
à 1, ce qui montre que l’information apportée par l’assimilation
d’un marégraphe côtier (en petits fonds donc) va avoir peu
d’influence sur la solution globale de marée, sauf autour de la
donnée assimilée. Les phases du représenteur montrent
clairement que la dynamique du modèle est conservée par ce
représenteur (Figure 50). En effet, nous retrouvons quantitativement
les phases de l’onde M2.
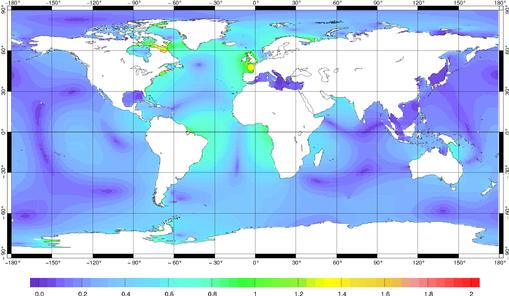
Figure 50 : Amplitude normalisée
du représenteur associé à la station de Port Tudy
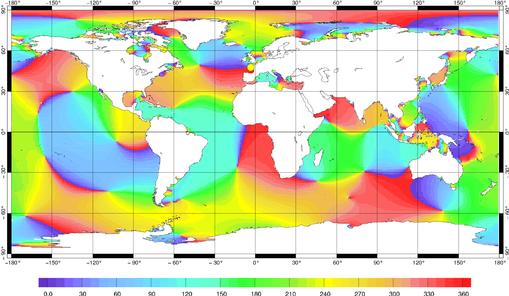
Figure 51 : Phase du représenteur
associé à la station de Port Tudy
11.2.2.2 Représenteur en zone
pélagique
Les mesures de la station marégraphique
IAPSO 1.4.32 sont représentatives de la marée en plein océan.
Ainsi, les mesures ne sont pas altérées par les interactions
entre les ondes principales. L’amplitude normalisée de ce représenteur
est beaucoup plus importante que celle de Port Tudy. En effet, elle n’est
pas supérieure à 1 qu’autour de la localisation du marégraphe
(point jaune), mais dans de nombreux bassins océaniques, en particulier
l’Atlantique et l’océan Indien (Figure 52). Plusieurs remarques
sont à faire. Le représenteur est important quand nous nous
rapprochons des côtes et donc des petits fonds : par exemple dans
le canal du Mozambique, le long des côtes occidentales de l’Inde
dans la mer d’Arabie, une portion du plateau de Patagonie, le long des
côtes orientales de l’Australie dans la mer de Corail et le détroit
de la baie d’Hudson dans l’Atlantique Nord. En outre, le représenteur
n’est pas maximum à l’emplacement du marégraphe, mais à
quelques centaines de kilomètres au sud. Enfin, nous pouvons noter
que l’amplitude du représenteur est peu importante dans l’océan
Pacifique. Ainsi, l’assimilation d’une donnée en plein océan
entraîne une propagation de l’information par le représenteur
beaucoup plus importante qu’en petits fonds. Cependant, comme l’analyse
harmonique d’une donnée en plein océan est beaucoup plus
fiable en plein océan, l’information propagée sera elle aussi
plus fiable qu’en milieu côtier. Nous vérifions encore que
la dynamique du problème est conservée en traçant
les phases du représenteur de la station IAPSO 1.4.32 (Figure 53).
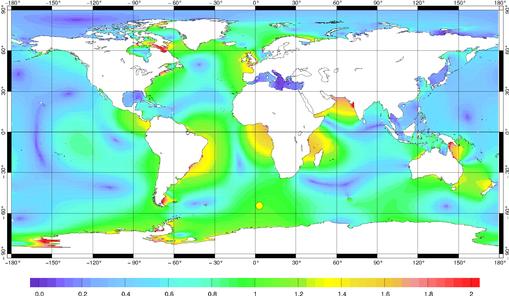
Figure 52 : Amplitude normalisée
du représenteur associé à la station IAPSO 1.4.32
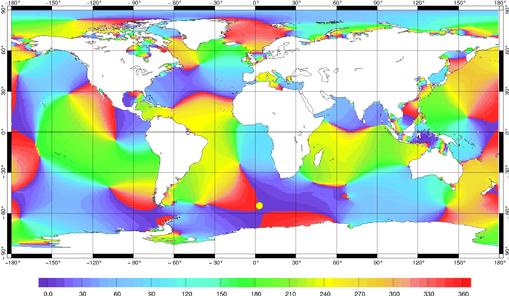
Figure 53 : Phase du représenteur
associé à la station IAPSO 1.4.32
11.2.2.3 Représenteur en zone
insulaire
Afin de bien saisir l’importance des représenteurs,
nous avons aussi étudié un représenteur associé
aux données d’un marégraphe placé sur une île
entourée de fonds profonds. C’est l’île de Saint Paul qui
a été choisie. Comme le montre l’amplitude normalisée
du représenteur de Saint Paul sur la Figure 54, ce dernier a une
influence globale que ce soit dans l’océan Indien, dans l’océan
Pacifique et dans une moindre mesure dans l’océan Atlantique. Comme
pour le représenteur de la station IAPSO 1.4.32, nous retrouvons
les mêmes caractéristiques en milieu côtier : de grandes
amplifications dans certaines zones (canal du Mozambique, côtes occidentales
de l’Inde dans la mer d’Arabie, plateau de Patagonie, détroit de
la Sonde, côtes orientales de l’Australie dans la mer de Corail,
mer de Ross, côtes occidentales de l’Amérique Centrale) qui
sont supérieures à l’amplitude de la donnée assimilée.
Les marégraphes localisés sur une île semblable à
celle de Saint Paul (ce qui est le cas de la majorité des îles
du Pacifique) ont donc des représenteurs associés qui ont
des caractéristiques semblables à ceux des marégraphes
de plein océan. Enfin les phases du représenteur de Saint
Paul sont une fois de plus en accord avec la dynamique de la propagation
de l’onde M2 sur l’océan mondial.
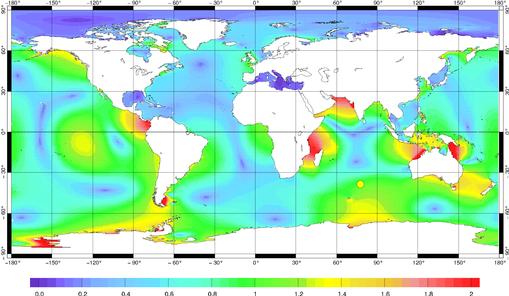
Figure 54 : Amplitude normalisée
du représenteur associé à la station de Saint Paul
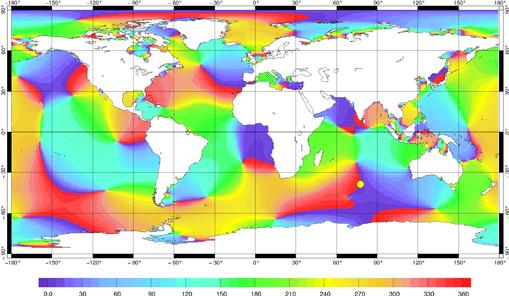
Figure 55 : Phase du représenteur
associé à la station de Saint Paul
11.2.3 Commentaires sur les représenteurs
Les représenteurs sont des champs qui
nous donnent les corrélations d’erreurs que propagent notre modèle
hydrodynamique à partir d’une position donnée sur toutes
les positions de l’océan mondial. Ainsi, si nous avons une forte
corrélation entre la position de la donnée assimilée
et un autre point, le calcul de la marée en cet autre point ne sera
pas dégradé si la donnée assimilée est bonne.
Nous aurons bien évidemment une solution dégradée
en ce point dans le cas où la donnée assimilée est
mauvaise. Il est donc essentiel d’assimiler des données de bonne
qualité (Bennet (communication personnelle, 1999) et Lefèvre
[1999a]).
Les caractéristiques que nous avons
dégagées ci-dessus sont valables pour l’ensemble des représenteurs
calculés pour produire FES98. Nous pouvons en tirer plusieurs commentaires.
Les données assimilées en petits fonds ne vont perturber
le calcul des solutions qu’autour de leur localisation. En effet la corrélation
des petits fonds avec les grands fonds est faible en regard de l’amplitude
de la donnée assimilée (nous avons représenté
les amplitudes normalisées des représenteurs). Ce qui permet
donc de régler localement l’erreur que nous devons associer à
la donnée. Comme les marégraphes côtiers mesurent un
spectre complexe de la marée, l’analyse est a priori moins fiable,
mais nous pouvons malgré tout donner une erreur relativement faible
puisque leur assimilation ne pourra pas trop dégrader la solution
de marée globalement. La précision de l’analyse harmonique
ne dépend pas du contenu fréquentiel, elle dépend
de l’erreur sur les mesures et de la durée de la série analysée.
En revanche pour les marégraphes de plein océan et sur les
îles, les mesures du spectre sont plus précises. Ainsi les
données assimilées sont a priori bonnes et nous pouvons donc
mettre une erreur faible sur les données assimilées. La qualité
de ces données est primordiale car comme l’a montré l’étude
précédente, la propagation de l’information assimilée
par le représenteur est quasiment globale. Une mauvaise donnée
assimilée en plein océan peu donc entraîner une dégradation
notable de la solution de marée le long des côtes. Un problème
réside cependant pour les données sur les îles. En
général, les données analysées de ces marégraphes
sont bonnes en amplitude, mais la configuration des îles entraîne
parfois un déphasage de l’onde par rapport à la propagation
en plein océan. Assimiler brutalement une donnée située
sur une île pourrait donc amener une erreur notable en phase. Nous
avons donc fixé une erreur plus importante pour ce type de donnée
que pour une donnée de type pélagique.
De plus, les tracés des représenteurs
associées aux trois types de données marégraphiques
(côtiers, grands fonds, îles) ont montré que ce n’est
pas forcément à l’endroit où la donnée est
assimilée que le représenteur est maximum. Nous retrouvons
à l’échelle globale les résultats que Egbert et
Bennet [1996] avaient découverts à l’échelle locale.
Ainsi, avec la méthode des représenteurs, l’assimilation
d’une donnée ne va pas forcément améliorer la solution
globale à l’endroit précis de la donnée. Pour améliorer
localement une solution, il faut donc prendre en compte la globalité
de la dynamique du modèle qui est intrinsèquement propagée
par les représenteurs.
La connaissance plus aboutie des représenteurs,
et donc des corrélations spatiales d’erreurs de notre modèle,
nous a permis de déterminer avec plus de rigueur les erreurs à
donner à nos données assimilées.
11.3 Données assimilées
Le Chapitre 10 a montré les qualités
de FES98 le long des côtes. Mais, comme nous l’avons déjà
souligné auparavant, cette solution présente un manque de
précision en plein océan. Afin de réduire ce manque,
nous avons entrepris l’assimilation de données altimétriques
qui ajoutent une densité spatiale conséquente à l’ensemble
des données que nous assimilons. Nous produisons ainsi FES99, une
solution hydrodynamique issue à la fois de données marégraphiques
(qui apportent une information importante sur les phénomènes
de marées en zones côtières) et de données altimétriques
(qui fournissent une information de qualité sur la propagation de
la marée en plein océan).
11.3.1 Données marégraphiques
Les données marégraphiques assimilées
sont majoritairement celles qui ont été utilisées
pour calculer les solutions de marées non altimétriques FES98
[Lefèvre et al., 2000a]. Cependant des problèmes majeurs
résidaient sur le plateau de Patagonie (dus à une bathymétrie
incertaine et des phénomènes de marées très
complexes et très importants dans cette zone : les élévations
peuvent atteindre plusieurs mètres le long des côtes). C’est
pourquoi, en fonction des travaux de Glorioso et al. [1997], une
sélection minutieuse de quelques données côtières
a été entreprise afin de les assimiler pour améliorer
les imperfections constatées. Ainsi, 20 données marégraphiques
ont été sélectionnées pour M2,
S2,
K1, O1 et Q1, 13
pour K2, 7 pour N2 et 5 pour 2N2
puis ont été assimilées. L’amélioration apportée
par l’assimilation de ces données est très bonne qualitativement
et quantitativement. En effet, les amplifications de marées qui
ont lieu dans le golfe de San Jorge et dans le Golfe de San Matias [Glorioso
and Flather, 1997] n’étaient pas modélisées dans
FES98. Elles le sont maintenant. Le Tableau 17 présente le nombre
de données marégraphiques assimilées.
|
Onde
|
Nombre de données assimilées
|
|
M2
|
783
|
|
S2
|
757
|
|
N2
|
636
|
|
K2
|
656
|
|
2N2
|
237
|
|
K1
|
897
|
|
O1
|
901
|
|
Q1
|
652
|
Tableau 23 : Nombre de données marégraphiques assimilées
suivant les ondes pour obtenir FES99
11.3.2 Données altimétriques
11.3.2.1 Origine des données
Une banque de composantes de la marée
issue de l’analyse des données de T/P a été construite
dans le cadre de notre étude (Schrama, communication personnelle,
1999). La grande majorité de ce paragraphe est issu d’un mémorandum
de Schrama. Les données sont situées aux points de croisement
de T/P c’est-à-dire aux points d’intersection d’une trace montante
et d’une trace descendante. Théoriquement, pour une répétition
cyclique de 10 jours (ce qui est approximativement le cas de T/P), le nombre
maximum de points de croisement est de 127². Environ 60% de ces points
sont situés sur des zones océaniques, l’autre partie étant
sur des terres émergées. La couverture de T/P ne s’étendant
pas jusqu’aux pôles, nous ne retrouvons pas le chiffre classique
de la couverture océanique sur la Terre, à savoir ~75%. Nous
avons utilisé les points de croisement par héritage des corrections
altimétriques faites auparavant et qui déjà utilisaient
les points de croisement (correction d’orbites…). Dans notre cas, nous
avons supposé que toutes les corrections autres que la marée
océanique et les effets de charges qui sont appliquées à
la mesure altimétrique et qui sont données par les GDR (Geophysical
Data Records) sont valides car calculées par d’autres scientifiques
et vérifiées. Les erreurs résiduelles sont considérées
comme trop faibles pour intervenir dans notre calcul de la marée
océaniques par l’altimétrie. Il faut noté que nous
avons appliqué les corrections de marées polaires et de marées
terrestres qui sont données par les GDR.
Traditionnellement, les données
aux points de croisement sont utilisées comme une observation de
différence de hauteur aux intersections des traces satellitales.
Dans notre étude, ce n’est pas nécessairement le cas car
chacune des données que nous générons est issue de
l’interpolation de plusieurs mesures autour du point d’intersection. La
méthode de calcul de la marée océanique aux points
de croisement est basée sur une orbite nominale représentant
la trace au sol de T/P plutôt que les positions réellement
observées. Cette source est appelée le ‘collinear stack file’
: elle est issue d’une collection de nombreux GDR gérée,
complétée et corrigée au Delft institute for Earth
Oriented Space research. De cette base de données nous avons calculé,
pour toutes les données T/P jusqu’au cycle 236, la trajectoire moyenne
au sol de T/P à des intervalles de 1 seconde par rapport au point
où la trace coupe l’équateur. Cette méthode d’interpolation,
dorénavant dénommée interpolation colinéaire,
est une procédure qui peut-être appliquée à
tous systèmes altimétriques survolant la Terre avec une répétitivité
constante. L’interpolation colinéaire suppose que la trace au sol
du satellite se répète suffisamment près d’un cycle
sur l’autre. Elle ne tient pas en compte les erreurs négligeables
habituelles introduites par les résidus dans le gradient spatial
du géoïde. Dans ce cas, l’erreur introduite par le gradient
résiduel r du géoïde est équivalent à
:
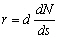 (11.132)
(11.132)
avec :
-
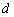 : la déviation moyenne de
la position de l’altimètre par rapport à la moyenne (meilleure
que 1 km pour T/P) ;
: la déviation moyenne de
la position de l’altimètre par rapport à la moyenne (meilleure
que 1 km pour T/P) ;
-
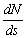 : la pente du géoïde.
: la pente du géoïde.
Dans les cas extrêmes, la pente peut
atteindre 10 m pour 100 km soit un gradient de 10-4. Dans la
plupart des parties de l’océan, il est de l’ordre de 10-5
ce qui entraîne une erreur inférieure à 1 cm pour l’interpolation
colinéaire. L’erreur introduite sur des zones de forte pente comme
les vallées et les monts sous-marins, est souvent plus élevées
d’un facteur 10. Ces évènements accidentels sont éliminés
par le moyen de procédures qui testent la répétitivité
des anomalies de mesures du niveau de la mer interpolées toutes
les secondes dans ‘collinear stack file’. Des 7990 points de croisement
théoriques, nous avons extrait grâce à cette procédure
7140 points de croisement de ce fichier. A chaque point de ce fichier,
nous obtenons des séries temporelles d’anomalies du niveau de la
mer mesurées par l’altimètre de T/P.
11.3.2.2 Correction du baromètre
inverse
Bien que la correction de baromètre
inverse soit donnée dans les GDR, nous avons appliqué une
procédure originale de calcul pour corriger la donnée altimétrique
de cet effet. En effet, nous avons jugé la correction insuffisante
pour nos besoins car les effets de baromètre inverse sont bien souvent
en phase avec l’onde de marée solaire S2 qui est
non seulement due au forçage gravitationnel mais aussi au forçage
radiationnel. C’est d’ailleurs la majeure contribution à la génération
de S2 en plein océan. Dans le cas courant, l’algorithme
calcule l’effet de baromètre inverse comme étant la réponse
hydrostatique locale calculée avec une pression atmosphérique
moyenne de référence égale à 1013.3 mbar. Dans
notre cas, nous nous sommes basés sur les données ECMWF de
la pression atmosphérique à la surface de la mer, moyennée
toutes les six heures.
11.3.2.3 Filtrage le long des traces
Nous savons que des phénomènes
de petits échelles interviennent dans les marées par la génération
d’ondes internes et qui sont visibles dans les anomalies de surface de
la mer. Ray et Mitchum [1996] ont montré que la puissance
moyenne de ces ondes se concentrent autour de longueur d'onde spatiale
de 100 km. Nous avons cherché à éliminer ces phénomènes
indésirables en introduisant une fenêtre de 20 secondes de
côté centrée à chaque position de points de
croisement. La Figure 56 illustre ce procédé.
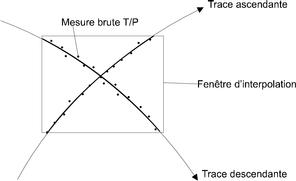
Figure 56 : Fenêtre de filtrage
des ondes internes dans l’analyse altimétrique des points de croisement
La longueur de la fenêtre correspond
approximativement à 150 km de chaque coté du point de croisement
que se soit pour la trace montante ou la trace descendante. Le but de cette
fenêtre est de sélectionner toutes les anomalies de surface
observées par T/P et de les introduire dans une procédure
d’estimation polynomiale. Ensuite, un filtrage par moindres carrés
permet de supprimer la partie barocline du signal de marée.
11.3.2.4 Génération
des données harmoniques altimétriques
Ainsi, des séries temporelles d’élévations
du niveau de la mer mesurées par les altimètres de T/P ont
été calculées. Ces données ont été
corrigée pour se rapporter à des mesures absolues du niveau
de la mer, référencées par rapport au géoïde
terrestre. Afin de construire des séries temporelles assez longues,
les points choisis furent les points de croisement des traces T/P : les
séries sont deux fois plus conséquentes. Après analyse
harmonique des séries temporelles en ces points, cette première
sélection a permis de construire une base de plus de 7140 points
donnant les amplitudes et les phases des ondes de marée M2,
S2,
N2, K2, K1,
O1,
P1 et Q1. Des corrections par comparaison
a priori et a posteriori des analyses ont permis de sélectionner
un nombre plus restreint de 5318 points (Figure 57).
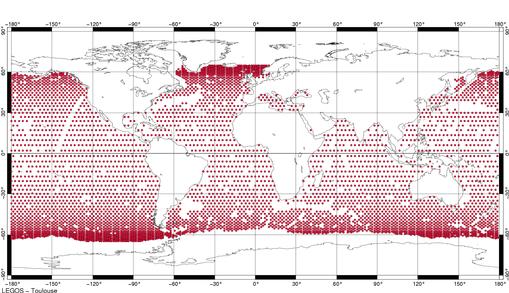
Figure 57 : Points de croisement sélectionnés
comme base de travail
11.3.2.5 Sélection des données
altimétriques à assimiler
La méthode d’assimilation est basée
sur la méthode des représenteurs qui sont significatifs de
la dynamique du modèle. Donc, en plein océan, deux représenteurs
associés à deux données assimilées très
proches spatialement l’une de l’autre (et en particulier en plein océan
où les interactions entre ondes de marées sont très
faibles) vont être similaires. Il n’est donc d’aucune utilité
de calculer tous les représenteurs associés à tous
les points de croisement pris en compte (les 5318 dans notre cas). Vu la
lourdeur des calculs et le temps nécessaire pour obtenir un représenteur,
il est préférable de sélectionner un certain nombre
de points caractéristiques à assimiler de l’ensemble de l’assimilation
comme l’ont déjà montré Egbert et al. [1994].
Ainsi nous sommes nous en partie restreints aux capacités de calculs
des supercalculateurs mis à notre disposition. Pour sélectionner
les points à assimiler à partir des 5318 à disposition,
plusieurs critères ont été mis en place :
§ Tous
les points en dehors des maillages éléments finis ont été
écartés car ils ne seraient de pas pris en compte dans l’assimilation.
§ Tous
les points placés au niveau de profondeurs inférieures à
200 mètres ont été éliminés. En effet,
les analyses de points de croisement dans les zones peu profondes sont
encore incertaines et, de plus, les données marégraphiques
assimilées, en particulier dans les petits fonds, comblent cette
lacune.
§ Une
distance minimale entre les points de croisement a été appliquée
afin d’éviter un sur-échantillonnage de points localement.
Cette distance a été fixée à 600 kilomètres
ce qui représente approximativement le double de la distance entre
deux traces T/P à l’équateur.
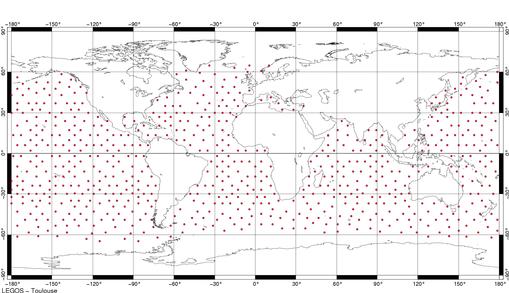
Figure 58 : Sélection des points
de croisement à assimiler
Ces critères ont permis d’extraire
687 points des 5318 initiaux (cf. Figure 58) et ont fourni l’amplitude
et la phase de la marée pour les 8 ondes citées auparavant.
Pour chacune des 7 ondes M2, S2, N2,
K2,
K1, O1 et Q1 les
687 représenteurs associés aux 687 localisations définies
ont été calculés.
Afin de rendre compte de la répartition
géographique de l’ensemble des données assimilées
pour le calcul de FES99, nous présentons Figure 59 cette répartition
pour l’onde M2. Nous pouvons voir que la répartition
spatiale est bien meilleure que celle utilisée pour le calcul des
solutions FES98.
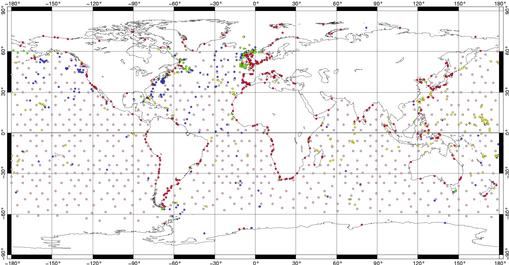
Figure 59 : Répartition géographique
de l’ensemble des points assimilés pour l’onde M2
11.3.3 Sélection des pondérations
pour l’assimilation
L’assimilation de données utilisée
dans notre étude est basée sur une technique d’inversion
avec une approche moindres carrés. Cette approche revient à
chercher la perturbation du modèle qui minimise une fonction coût
J introduite dans le Chapitre 9 et que nous rappelons ici :
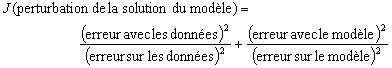
Il faut donc déterminer les erreurs
sur les données et sur le modèle.
11.3.3.1 Erreurs sur les données
Des comparaisons avec d’autres modèles
ainsi que des mesures de terrains permettent de fixer une erreur (inverse
de la confiance) sur les données en fonction de leur localisation.
Ainsi, de même que pour le calcul de FES98, nous avons créé
5 catégories de données, en fonction de la bathymétrie,
du profil des côtes et de l’origine des données :
-
la catégorie côtière (coastal) ;
-
la catégorie de plateau (shelf) ;
-
la catégorie pélagique (pelagic) ;
-
la catégorie insulaire (island) ;
-
la catégorie altimétrique (altimetry) ;
A ces 5 catégories nous avons associé
une confiance aux données, fixée par expérience des
mesures et par plusieurs calculs d’assimilation.
Pour les ondes M2, S2,
N2,
K2, 2N2, K1, O1, Q1
nous avons pris une confiance de :
-
2,5 centimètres en catégorie côtière ;
-
1 centimètre en catégorie de plateau ;
-
0,5 centimètre en catégorie pélagique ;
-
2,5 centimètres en catégorie insulaire ;
-
0,75 centimètre en catégorie altimétrique.
Ces erreurs sont bien en accord avec les conclusions
de notre étude sur les représenteurs, à savoir que
l’analyse d’une donnée étant bonne en plein océan
et que sa corrélation spatiale étant importante avec les
autre points de l’océan, nous lui avons fixé une confiance
élevée (et donc une faible erreur). Par contre, du fait des
problèmes liés aux phases avec les données des îles,
nous ne leur avons donné qu’une erreur de 2,5 cm. Pour les données
de plateaux et les données côtières, nous avons gardé
les erreurs utilisées dans FES98. Enfin, pour les données
altimétriques, une erreur de 0,75 cm est raisonnable, puisque le
but des mesures T/P est d’atteindre la précision centimétrique.
Nous avons vérifié que ces erreurs sont consistantes avec
l’assimilation en vérifiant en chaque donnée que le modèle
a posteriori donne environ la valeur de l’observation plus ou moins l’erreur
fixée a priori.
11.3.3.2 Erreurs sur le modèle
La méthode d’assimilation est à
contrainte faible, c’est-à-dire que nous prenons en considération
l’erreur du modèle. Cette erreur est principalement due à
une erreur sur le forçage qui ne peut pas être quantifiée.
C’est pourquoi, nous avons sélectionné l’erreur à
donner au modèle par plusieurs assimilations successives qui nous
ont permis de la fixer en comparant la solution a priori (qui est purement
hydrodynamique c’est-à-dire sans assimilation ) par rapport à
la solution a posteriori (qui est la solution assimilée). En effet,
la procédure d’assimilation nous donne accès à un
certain nombre d’outils nous permettant de vérifier sa qualité
a posteriori, et donc d’avoir une idée de l’erreur à appliquer
au modèle. Le calcul de la fonction coût est le rapport du
signal sur le bruit. Il nous permet de quantifier l’assimilation, sachant
que le cas idéal est atteint pour un rapport de 100%.
|
Ondes
|
Rprior
|
Rposterior
|
Coefficient modèle
|
|
M2
|
1738%
|
103%
|
3x10-3
|
|
S2
|
882%
|
107%
|
1x10-3
|
|
N2
|
349%
|
87%
|
3x10-4
|
|
K2
|
236%
|
107%
|
1x10-4
|
|
2N2
|
52%
|
42%
|
1x10-2
|
|
K1
|
324%
|
98%
|
2x10-3
|
|
O1
|
332%
|
103%
|
5x10-4
|
|
Q1
|
108%
|
80%
|
5x10-4
|
Tableau 24 : Rapport signal bruit avant et après assimilation
Le rapport a priori Rprior
est l’écart type entre les erreurs du modèle a priori et
les erreurs des données assimilées. Une valeur de 100% indique
que le modèle a priori et les observations ne sont pas significativement
différents. Le rapport a posteriori Rposterior
est l’écart type entre les erreurs de la solution a posteriori (c’est-à-dire
la solution assimilée) et l’écart type des erreurs des données
assimilées. La dernière colonne du tableau indique le coefficient
qui a été donné à l’erreur sur le modèle
pour atteindre au mieux les 100% de Rposterior grâce
à l’assimilation.
Nous pouvons voir que les 100% ne sont
pas atteints dans tous les cas. En effet, les rapports introduits ci-dessus
ne sont pas absolus pour représenter le bon déroulement de
l’assimilation, mais ils sont un bon indicateur pour fixer les erreurs
modèle.
11.4 Calcul des solutions
11.4.1 Ondes principales
Avec la même approche que celle utilisée
pour FES98, nous avons calculé les ondes principales du spectre
de marée, à partir des solutions libres de notre modèle
hydrodynamique que nous avons amélioré par l’assimilation
de données marégraphiques et altimétriques.
|
Onde
|
Nombre de données assimilées
|
|
M2
|
1470
|
|
S2
|
1444
|
|
N2
|
1323
|
|
K2
|
1343
|
|
2N2
|
237
|
|
K1
|
1584
|
|
O1
|
1588
|
|
Q1
|
1339
|
Tableau 25 : Nombre de données assimilées suivant les
ondes pour obtenir FES99
A titre d’illustration, nous donnons la
distribution de l’onde M2 (Figure 60 et Figure 61)et
de l’onde K1 (Figure 62 et Figure 63) en amplitude et
en phase à l’échelle globale. Ces figures sont représentatives
du phénomène de propagation des ondes de marées semi-diurnes
et diurnes. En particulier, nous pouvons voir grâce qu réseau
de phase de l’onde M2 que la dynamique du problème
hydrodynamique est bien conservé dans les représenteurs (cf.
–phase des Figure 51 et Figure 53 et Figure 55).
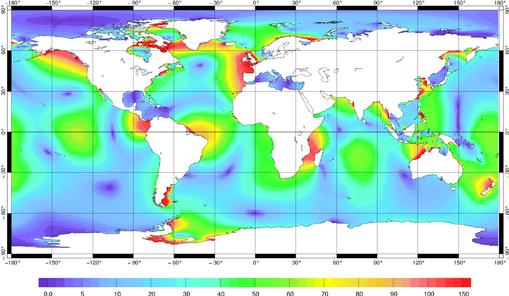
Figure 60 : Amplitude de M2
(cm) pour FES99
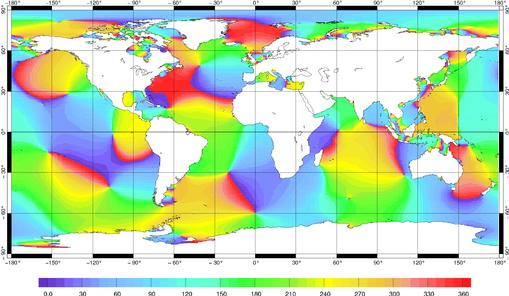
Figure 61 : Phase de M2
(degrés) pour FES99
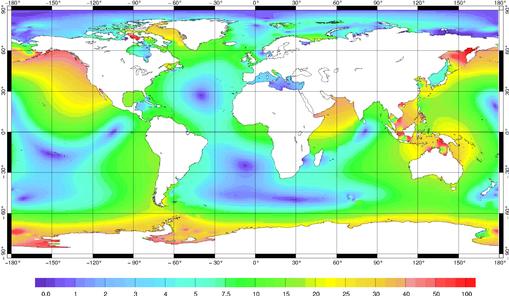
Figure 62 : Amplitude de K1
(cm) pour FES99
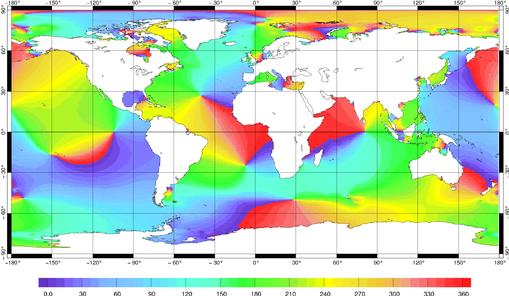
Figure 63 : Phase de K1
(degrés) pour FES99
Afin de rendre compte des améliorations
apportées par l’assimilation de données altimétriques
dans notre modèle, nous comparons FES98 et FES99 par rapport à
trois banques : ST95, ST727 et la banque de données Topex introduite
au paragraphe 10.4.1.3.
11.4.1.1 Comparaisons aux données
marégraphiques pélagiques
Par comparaison avec ST95, le Tableau 26 montre
que FES98 est meilleure que FES99 pour toutes les ondes sauf M2.
Le fait d’avoir reconsidéré les paramètres de l’assimilation
(erreurs sur le modèle et erreurs sur les données) a permis
d’améliorer l’onde M2 de 14%. Les autres ondes
n’ont pu être améliorées, car comme nous avons assimilé
beaucoup de données en plein océan avec l’altimétrie,
nous avons réduit le poids que nous donnions aux données
de ST95 (située majoritairement en zones pélagiques) qui
sont à la fois assimilées et utilisées dans la comparaison.
Cependant, la RSS globale, du fait de l’amélioration notable de
FES99 pour M2, est meilleure que celle de FES98 (6 petits
dixièmes de millimètre…)
|
Onde
|
RMS sur les données (cm)
|
Nombre de données
|
FES98
RMS (cm)
|
FES99
RMS (cm)
|
|
M2
|
33,55
|
95
|
1,51
|
1,30
|
|
S2
|
12,81
|
95
|
0,86
|
0,87
|
|
N2
|
6,79
|
91
|
0,80
|
0,82
|
|
K2
|
3,32
|
90
|
0,35
|
0,38
|
|
2N2
|
1,01
|
90
|
0,31
|
0,33
|
|
K1
|
11,10
|
95
|
1,00
|
1,09
|
|
O1
|
7,66
|
95
|
0,93
|
0,96
|
|
Q1
|
1,61
|
87
|
0,25
|
0,27
|
|
RSS (cm)
|
-
|
-
|
2,41
|
2,35
|
Tableau 26 : Comparaisons numériques pour ST95
11.4.1.2 Comparaisons aux données
côtières
L’assimilation de données marégraphiques
côtières a montré que FES98 améliorait notre
connaissance des marées en petits fonds. Comme nous assimilons les
mêmes données en plus des données altimétriques,
les comparaisons le long des côtes nous permettent de vérifier
que l’assimilation de données altimétriques en plein océan
n’a pas altéré la qualité de la solution en petit
fond. Comme nous avions des problèmes avec FES98 sur le plateau
de Patagonie, nous avons ajouté 12 marégraphes de comparaison
le long des côtes de la Patagonie à la banque de données
ST727 pour former une banque plus complète : ST739.
|
Onde
|
RMS sur les données (cm)
|
Nombre de données
|
FES98
RMS (cm)
|
FES99
RMS (cm)
|
|
M2
|
60,30
|
739
|
17,49
|
10,58
|
|
S2
|
22,22
|
737
|
6,28
|
5,39
|
|
N2
|
12,48
|
625
|
4,74
|
3,95
|
|
K2
|
6,58
|
628
|
2,39
|
2,27
|
|
2N2
|
1,84
|
263
|
1,07
|
1,03
|
|
K1
|
13,47
|
736
|
4,83
|
4,24
|
|
O1
|
9,75
|
732
|
3,61
|
3,26
|
|
Q1
|
2,01
|
403
|
1,11
|
1,01
|
|
RSS (cm)
|
-
|
-
|
20,30
|
13,87
|
Tableau 27 : Comparaisons numériques pour ST739
Le Tableau 27 montre que globalement, FES99
est meilleure que FES98 pour toutes les ondes, comparée à
ST739. Cependant ST739 est identique à ST727 avec l’ajout de données
de comparaisons le long des côtes du plateau de Patagonie où
les ondes de marées peuvent prendre des valeurs assez importantes
(plusieurs mètres). Comme FES98 n’est pas de très bonne qualité
dans cette zone, sa comparaison à ST739 est moins bonne que celle
de FES99. C’est pourquoi, nous avons aussi comparé FES99 à
ST727 pour apprécier sa qualité par rapport à FES98
le long des côtes de l’océan mondial.
|
Onde
|
RMS sur les données (cm)
|
Nombre de données
|
FES98
RMS (cm)
|
FES99
RMS (cm)
|
|
M2
|
57,78
|
727
|
10,99
|
10,30
|
|
S2
|
22,04
|
725
|
5,56
|
5,35
|
|
N2
|
12,18
|
617
|
3,66
|
3,34
|
|
K2
|
6,54
|
616
|
2,24
|
2,26
|
|
2N2
|
1,84
|
263
|
1,09
|
1,03
|
|
K1
|
13,48
|
724
|
4,71
|
4,24
|
|
O1
|
9,74
|
720
|
3,56
|
3,22
|
|
Q1
|
2,01
|
402
|
1,11
|
1,01
|
|
RSS (cm)
|
-
|
-
|
14,40
|
13,47
|
Tableau 28 : Comparaisons numériques pour ST727
Ainsi, d’après le Tableau 28, FES99
reste la meilleure des deux solutions au niveau global le long des côtes
pour toutes les ondes exceptée K2. Le fait d’avoir
modifié l’erreur sur le modèle, bien qu’en ayant assimilé
des données altimétriques en plein océan, a amélioré
la qualité de FES99 le long des côtes. La RSS est meilleure
de 6,5%.
11.4.1.3 Comparaisons à l’altimétrie
Des comparaisons avec la banque de données
Topex nous montrent clairement les améliorations qu’apporte l’assimilation
de données altimétriques dans FES99 par rapport à
FES98 (cf. Tableau 29) : 64% pour M2 et 42% pour K1.
Ainsi la RSS de FES99 est 42% meilleure que celle de FES98.
|
Onde
|
RMS sur les données (cm)
|
Nombre de données
|
FES98
RMS (cm)
|
FES99
RMS (cm)
|
|
M2
|
25,85
|
5313
|
2,51
|
0,91
|
|
S2
|
9,71
|
5313
|
1,19
|
0,68
|
|
N2
|
5,59
|
5313
|
0,82
|
0,65
|
|
K2
|
2,83
|
5313
|
0,98
|
0,89
|
|
2N2
|
-
|
-
|
-
|
-
|
|
K1
|
10,00
|
5313
|
1,61
|
0,94
|
|
O1
|
7,20
|
5313
|
1,14
|
0,80
|
|
Q1
|
1,70
|
5313
|
0,83
|
0,80
|
|
RSS (cm)
|
-
|
-
|
3,73
|
2,16
|
Tableau 29 : Comparaisons numériques pour la banque Topex
11.4.2 Ondes secondaires
Pour étendre le spectre de marée,
nous avons calculé les ondes secondaires m2,
n2,
L2,
l2,T2,
e2,
h2,
P1,
2Q1, r1,
s1,
J1, c1,
M11,
M12, OO1, j1,
p1,
et q1
par la méthode d’admittance mise en place dans le chapitre précédent.
Nous donnons dans le Tableau 30 les comparaisons de ces ondes secondaires
avec la banque ST95. Cette banque étant composée de marégraphes
avec de longues périodes de mesures dont l’analyse harmonique est
de qualité, elle nous donne accès à de nombreuses
ondes secondaires.
|
Onde
|
RMS sur les données (cm)
|
Nombre de données
|
FES98
RMS (cm)
|
FES99
RMS (cm)
|
|
m2
|
1,20
|
90
|
0,39
|
0,39
|
|
n2
|
1,27
|
90
|
0,16
|
0,16
|
|
L2
|
0,89
|
89
|
0,25
|
0,25
|
|
l2
|
0,27
|
16
|
0,21
|
0,21
|
|
T2
|
0,76
|
89
|
0,16
|
0,17
|
|
e2
|
0,29
|
19
|
0,15
|
0,17
|
|
h2
|
0,34
|
7
|
0,19
|
0,19
|
|
P1
|
3,57
|
90
|
0,39
|
0,39
|
|
2Q1
|
0,22
|
8
|
0,15
|
0,15
|
|
r1
|
0,20
|
9
|
0,10
|
0,10
|
|
s1
|
0,18
|
10
|
0,10
|
0,11
|
|
J1
|
0,55
|
29
|
0,29
|
0,29
|
|
c1
|
-
|
0
|
-
|
-
|
|
M11
|
-
|
0
|
-
|
-
|
|
M12
|
-
|
0
|
-
|
-
|
|
OO1
|
0,29
|
24
|
0,21
|
0,21
|
|
j1
|
0,31
|
9
|
0,29
|
0,29
|
|
p1
|
0,31
|
10
|
0,29
|
0,29
|
|
q1
|
0,17
|
7
|
0,15
|
0,15
|
|
RSS
|
-
|
-
|
0,94
|
0,95
|
Tableau 30 : Comparaisons numériques des ondes secondaires
pour la banque ST95
Ainsi, la précision des ondes principales
nous permet d’obtenir des ondes secondaires de bonne qualité. En
outre, comparée à ST95, FES99 est pratiquement de la même
précision que FES98. Les RSS sont identique à un dixième
de millimètre seulement.
11.4.3 Code de prédiction
Les chapitres précédents nous
l’ont montré, la marée se décompose en sommes de composantes
harmoniques. Afin d’obtenir la marée en un lieu et une date donnés,
il faut donc reconstituer le signal à partir de ces composantes
dépendant de la latitude, de la longitude et du temps. Grâce
à la théorie de Doodson complétée par
les calculs scientifiques de Schureman, nous sommes à même
de proposer un code de prédiction qui nous donne la hauteur de la
marée océanique en toute position de la surface océanique
et à tout moment. Afin de tester ces codes de prédictions
nous comparons la réduction de variance qu’ils apportent en plus
des autres corrections des GDR. En effet, en soustrayant le signal brut
altimétrique de toutes les corrections apportées par les
GDR, nous accédons (en théorie) au signal océanique.
En prenant en compte toutes les corrections des GDR et en remplaçant
la correction de marée par le calcul que nous avons fait avec notre
code de prédiction, nous obtenons la hauteur de mer due au signal
océanique plus le bruit et les erreurs dans les corrections. Donc
a priori plus la variance calculée est faible, meilleur est le modèle
car nous avons moins d’erreur sur notre modèle. Il faut cependant
noter que la plus basse des variances calculées avec un modèle
ne donne pas forcément le choix pour le meilleur modèle si
ce modèle de marée océanique a assimilé de
l’information océanique autre que la marée. Cependant, les
modèles FES étant issus de méthodes semblables et
étant largement basés sur des équations hydrodynamiques
qui conservent l’information physique des marées, nous ferons abstraction
de ce cas. Il n’en est pas de même si nous utilisons des modèles
empiriques qui sont exclusivement issus des données altimétriques.
En effet ces derniers, si l’analyse de marée qui a permis de les
calculer a été mal faite et contient donc du signal océanique,
vont donner une plus faible variance, mais ne donneront pas forcément
accès au signal océanique puisqu’il aura été
inclus dans le signal de marée fourni par le modèle.
Nous avons comparé les trois modèles
FES95.2, FES98 et FES99 par rapport aux données fournies par les
deux satellites T/P et ERS-2. Le modèle FES94.1 n’a pas été
pris en considération dans cette étude car il ne présente
pas assez de composantes de marée pour pouvoir donner un code de
prédiction de marée suffisamment précis. Pour T/P,
nous avons considéré les cycles 95 (13 avril 1995) à
195 (10 janvier 1998) et pour ERS-2, les cycles 0 (29 avril 1995) à
28 (19 janvier 1998). Ces cycles ont été sélectionnés
car ils représentent plus de deux ans de données, car ils
se chevauchent pour les deux satellites et car ils ont permis de conserver
des temps de calculs raisonnables. Pour chaque cycle, ~4x105
(respectivement ~14x105) points étaient disponibles pour
les comparaisons avec les données T/P (respectivement ERS-2). Le
nombre important de données nous laisse supposer de la bonne qualité
des tests. Nous avons ainsi calculé l’écart type (racine
carrée de variance) pour chacun des trois modèles FES les
autres corrections des GDR étant constantes. Les données
altimétriques sont référencées par rapport
au géoïde et non par rapport à la topographie dynamique.
Il faut donc tenir compte des effets de charges dans nos calculs. Afin
de rester cohérent avec ces effets de charges, Francis (communication
personnelle, 1995, 1999, 2000), nous a calculé les effets de charge
déduits de chacun des trois modèles. Pour chacun des modèles,
nous avons donc retiré les effets de charges associés pour
le calcul de l’écart type. Les résultats numériques
sont donnés dans le Tableau 31. Les codes de calcul utilisés
pour obtenir les écarts types ont été développés
par la Division de l’Océanographie Spatiale de CLS et utilisés
à CLS.
|
Solution
|
Ecart-type (cm)
pour T/P
|
Ecart type (cm)
pour ERS-2
|
|
FES95.2
|
11,33
|
12,38
|
|
FES98
|
10,94
|
12,09
|
|
FES99
|
10,66
|
11,79
|
Tableau 31 : Ecart type des résidus du signal altimétrique
le long des traces T/P et ERS-2
FES99 apparaît donc comme donnant
le plus faible écart type pour T/P (~5,9% plus faible que pour FES95.2
et ~2,6% plus faible que pour FES98), de même que pour ERS-2 (~4,8%
plus faible que pour FES95.2 et ~2,5% plus faible que pour FES98). Cependant,
ces résultats sont globaux et ne rendent pas compte des améliorations
locales. En outre, FES99 contient de l’information assimilée issue
du satellite T/P : les données ERS-2 s’avèrent donc être
une base de données indépendante de nos modèles FES.
C’est pourquoi, nous avons tracé à l’échelle globale
les écarts types des résidus d’anomalies de surface entre
la solution FES99 et les deux autres solutions FES (Figure 64 pour FES95.2
et Figure 65 pour FES98). Ces figures rendent ainsi mieux compte des améliorations
globales tout en mettant l’accent sur les différences locales.
Plus les figures sont bleues, plus l’écart
type de l’anomalie de niveau de la mer calculée avec FES99 comme
correction de marée est faible. Donc plus FES99 est adaptée
à la réduction de l’écart type et plus l’erreur faite
sur la marée est faible parmi les corrections du GDR.
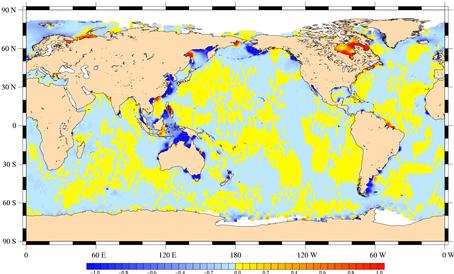
Figure 64 : Ecart type entre les résidus
calculés avec FES99 et FES95.2
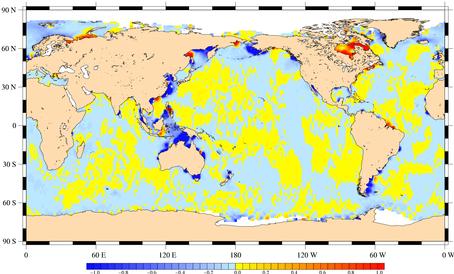
Figure 65 : Ecart type entre les résidus
calculés avec FES99 et FES98
Les différences résiduelles
sont majoritairement situées autour de 0 cm (entre +/- 0,05 cm)
ce qui est très faible comparé à l’ordre de grandeur
de 10 cm donné par le Tableau 31. Cependant, des deux figures précédentes,
il ressort des zones de fortes variations entre FES99 et les deux autres
solutions FES. Intéressons-nous de plus près aux différences
de résidus entre FES99 et FES95.2. En plein océan, nous pouvons
constater que les deux solutions sont quasiment identiques. Des différences
de l’ordre de +/-1 cm sont localisées le long de certaines côtes
de l’océan mondial, sur quelques plateaux continentaux et dans quelques
mers fermées. L’écart type calculé avec FES99 est
inférieur à –1 cm (bleu profond) de celui calculé
avec FES95.2 dans le détroit du Sri Lanka, la partie orientale de
la Mer d’Andaman, le Golfe du Tonkin, la Mer de Chine Orientale, la Mer
Jaune, la Mer de Sulu, la Mer des Célèbes, la Mer de Timor,
une grande partie des côtes australiennes, les partie orientales
des Mers d’Okhotsk et de Béring, le Golfe de Californie, le plateau
de Patagonie, le détroit du Danemark, la Mer de Norvège,
la Mer d’Irlande et les parties occidentale et orientale de la Mer du Nord.
Mais il y existe des zones où l’écart type des résidus
est supérieur à 1 cm, c’est-à-dire des zones ou la
prédiction réalisée avec FES99 serait moins que celle
réalisée avec FES95.2 : la zones parmi les îles indonésiennes,
l’embouchure de l’Amazone, le sud de mer de Barents, une petite partie
occidentale des Mers d’ Okhotsk et de Béring et la baie d’Hudson.
Cependant pour les zones des Philippines et de l’Amazone, nous savons que
la structure complexe des terres émergées et des faibles
fonds marins empêche d’accéder à des mesures altimétriques
précises. Les zones de Barents, Okhotsk, Béring et Hudson
posent un autre problème avec les glaces qui apparaissent durant
les périodes plus froides au cours des années. En effet la
couche de glace qui se forme sur ces eaux pollue la mesure altimétrique
au cours d’une année et les comparaisons avec nos modèles
FES sont donc biaisées. Malgré tout, ces comparaisons entre
FES99 et FES95.2 montrent de manière générale que
les améliorations réalisées pour FES99 ont porté
leurs fruits puisque FES99 donne de plus faibles résidus pour le
signal altimétrique corrigé que FES95.2 dans des zones connues
pour être moins bien modélisées du point de vue des
marées océaniques. En outre les phénomènes
de résonances constatés dans FES95.2 sont maintenant corrigés
dans FES99. Les comparaisons des résidus entre FES99 et FES98 montrent
que FES99 est de meilleure qualité a peu près partout sauf
dans la Mer de Chine Orientale et la Mer de Béring. Contrairement
aux comparaisons avec FES95.2, les différences sont plus lisses
et plus faibles, ce qui est certainement dû à la similarité
de la méthode d’assimilation qui en petits fonds n’utilise que des
données marégraphiques communes à la génération
de FES98 et FES99. Dans ces zones de petits fonds (inférieurs à
200 m) aucune donnée altimétrique n’a été assimilée.
11.5 Bilan sur FES99
La révision et l’amélioration
du code d’assimilation nous ont permis d’obtenir une nouvelle solution
de marée FES99 utilisant des données marégraphiques
et altimétriques. Les données déjà assimilées
dans FES98 ont été complétées par des données
marégraphiques sur le plateau de Patagonie. Les données altimétriques
sont issues de l’analyse des données T/P aux points de croisements.
L’amélioration par rapport à FES98 est assez importante particulièrement
en plein océan. La compréhension des erreurs de covariances
intégrées dans les représenteurs a permis de ne pas
dégrader les solutions le long des côtes. Ainsi FES99 fournit
un spectre de marée complet avec huit principales M2,
S2,
N2, K2, 2N2,
K1,
O1 et Q1 et 19 ondes secondaires m2,
n2,
L2,
l2,T2,
e2,
h2,
P1,
2Q1, r1,
s1,
J1, c1,
M11,
M12, OO1, j1,
p1,
et q1.
Pour compléter ce spectre, les 3 ondes longues périodes de
FES98 ont été ajoutées : Mf, Mm
et Mtm. Comme pour FES98, ces nouvelles solutions éléments
finis ont été projetées sur des grilles régulières
et sont disponibles sur des grilles de 0,25°x0,25°.
Cette nouvelle solution de marée
[Lefèvre et al., 2000b] est en cours de validation dans le
choix du meilleur modèle à utiliser pour les corrections
de marée des futures données du satellite Jason.
Back |
Next
Title: Thèse de Fabien Lefèvre
Issue: Version 1.0
Date: 29/09/2000
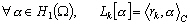 (11.131)
(11.131)
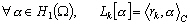 (11.131)
(11.131)
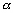 : le champ de dénivellation
(de dimension le nombre de nœuds du maillage) ;
: le champ de dénivellation
(de dimension le nombre de nœuds du maillage) ;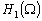 : l’espace des dénivellations
;
: l’espace des dénivellations
;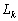 : la fonctionnelle linéaire
qui au champ
: la fonctionnelle linéaire
qui au champ 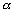 associe la dénivellation
au point de la donnée assimilée k ;
associe la dénivellation
au point de la donnée assimilée k ; : le produit scalaire prenant en
compte les erreurs sur le modèle.
: le produit scalaire prenant en
compte les erreurs sur le modèle.





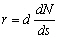 (11.132)
(11.132)
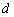 : la déviation moyenne de
la position de l’altimètre par rapport à la moyenne (meilleure
que 1 km pour T/P) ;
: la déviation moyenne de
la position de l’altimètre par rapport à la moyenne (meilleure
que 1 km pour T/P) ;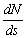 : la pente du géoïde.
: la pente du géoïde.