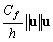Chapitre 12 Améliorations du modèle hydrodynamique
global en zone littorale
12.1 Présentation du chapitre
En plus de notre travail de construction de
nouvelles solutions globales de marées, nous avons entrepris des
études afin d’améliorer notre modèle hydrodynamique
le long des côtes. Nous avons déterminé dans le Chapitre
6 quels sont les différents paramètres d’entrée du
modèle qui influent sur le calcul des marées par le code
CEFMO. Or nous avons montré dans les deux chapitres précédents
que nos solutions globales de marées sont de bonne précision
grâce à l’assimilation de données mesurées in
situ. Si nous voulons obtenir un modèle hydrodynamique de qualité
en utilisant aucune mesure et si nous voulons que sa précision soit
celle des modèles assimilant des données, il nous faut donc
étudier la qualité d’une solution de marée issue de
CEFMO en fonction de la variation de différents paramètres
(bathymétrie, effets de charge et d’auto-attraction, coefficient
de Chézy, résolution du maillage, frontières ouvertes…).
Une étude globale est difficilement possible si nous voulons étudier
toutes les différences qu’impliquent les variations des paramètres
d’entrée du modèle. C’est pourquoi, nous avons tous nos tests
sur un bassin local. La Mer Jaune et la Mer de Chine Orientale forment
un excellent bassin test du fait de la faible profondeur et de la forte
dissipation énergétique de marée qui y prend place.
Le but de ce chapitre est d’utiliser cette zone afin de déterminer
les améliorations à apporter à notre modèle.
Nous allons d’abord introduire la zone
d’étude et la base de données marégraphiques qui va
nous permettrent de comparer nos solutions. Puis nous examinerons précisément
les paramètres physiques et numériques qui affectent la qualité
du modèle hydrodynamique éléments finis, à
savoir les conditions aux limites, le mode de calcul, la résolution
du maillage et les variations du coefficient de frottement. Nous n’apporterons
que des améliorations physiques au modèle hydrodynamique.
Aucune assimilation de donnée ne sera effectuée. La qualité
du modèle dans cette zone locale ne sera donc que la conséquence
des améliorations des paramètres d’entrée du code.
Enfin, nous établirons un bilan énergétique sur la
zone en comparant nos champs de vitesses avec des courantomètres
de pleine eau, afin de mieux comprendre la dissipation due au frottement
sur le fond dans le cas de notre modèle.
Cette étude nous permet de fournir
les solutions des principales ondes du spectre de marées :
-
M2, S2, N2, K2
et 2N2 pour les composantes semi-diurnes ;
-
K1, O1, P1 et Q1
pour les composantes diurnes ;
-
M4 et MS4 pour les composantes quart-diurnes.
12.2 Choix de la zone d’étude
12.2.1 Introduction
L’objet de l’étude est de savoir ce
que nous pouvons attendre des améliorations du modèle hydrodynamique
dans une zone littorale. Nous avons décidé de nous focaliser
sur la Mer Jaune et la Mer de Chine Orientale (en anglais ‘Yellow Sea and
the East China Sea’ et dès à présent résumé
par YS-ECS). Nous avons plusieurs raisons pour sélectionner cette
zone, la principale étant que le modèle hydrodynamique FES94.1
présente certaines lacunes comparées à d’autres zones
comme le plateau européen où FES94.1 est correct [Andersen
et al., 1995]. Nous nous sommes donc interrogés sur les différences
de qualité qui peuvent exister entre deux zones avec le même
modèle. Les marées sont importantes dans YS-ECS. La Navy
anglaise [Hydrographer of the Navy, 1992] indique que les élévations
de marées peuvent atteindre environ 5,6 m sur la côte ouest
de Taiwan (à côté de Chang Hua à 150 kilomètres
au sud ouest de Taipei), 3 m dans la baie de Hanchow (près de Shanghai),
3,7 m dans la baie de Pohai Bay (près de Pékin), et 8.5 m
dans la baie de Incheon (à l’Ouest de Séoul en Corée
du Sud). Les courants de marée peuvent atteindre de grandes valeurs
: une étude commandée par une centrale électrique
coréenne [Korea Electric Company, 1978] rapporte qu’ils peuvent
atteindre 3 m s-1 à l’entrée de la baie de Cheonsu
durant les marées d’équinoxes. Les valeurs considérables
de ces élévations et de ces vitesses de marées prouvent
que cette zone est une des régions océaniques où la
dissipation de la marée est très importante. Une des premières
estimations de la dissipation pour la composante M2 a
été donnée par Miller [1966], qui a conclu
que 60 Giga watts (GW) sont dissipés dans la Mer Jaune seule, ce
qui représente 3,5% des 1,7 Téra watts (TW) qu’il estimait
pour la dissipation globale par le frottement sur les fonds océaniques
à l’échelle globale. De nouvelles estimations de Le Provost
et Lyard [1997]estiment la dissipation de M2 à
180 GW sur cette zone, soit 11,1% des 2 TW globaux estimés pour
la dissipation de la friction de fond. Kantha et al. [1995] ont
obtenu la même valeur. Dans ce cas, quelles valeurs sont les bonnes?
Toutefois, nous savons qu’elles sont dépendantes de la qualité
des solutions en courant et du choix du coefficient de frottement utilisé
pour paramétriser cette dissipation.
12.2.2 Description de la zone
Cette zone (cf. Figure 66) est divisée
en 4 parties différentes :
-
à la latitude de Pékin, la baie de Pohai (Bo Hai) ;
-
à l’ouest de la Corée du Sud, la Mer Jaune (Huang Hai) ;
-
au nord de Taiwan, la Mer de Chine Orientale (Dong Hai) ;
-
au sud de Taiwan, une partie de la Mer de Chine Méridionale (Nan
Hai).
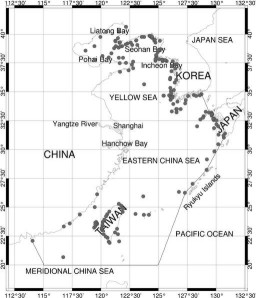
Figure 66 : Carte de la zone d’étude
et marégraphes utilisés dans les comparaisons
Cette zone est très complexe, à
la fois à cause de la topographie (cf. Figure 67), mais aussi à
cause de la dynamique locale des marées. En effet, elle est parsemée
de bancs de sable, de récifs, d'îles, de courants changeants
et rapides. Au nord, le littoral de la péninsule coréenne
et la côte orientale de la Mer de Grêle jusqu'à la hauteur
de Shanghai présente un relief plat, rectiligne, sablonneux et une
mer avec peu d'îles au large. Au sud de Shanghai, les rivages sont
plus découpés : collines, éperons rocheux et îlots.
La plupart du temps, il s'agit de récifs coralliens affleurants.
Alentour, plusieurs fosses atteignent 4000 mètres. L'extension en
latitude explique les écarts de températures : la baie de
Pohai est prise par l'embâcle jusqu'en mars, ce qui nécessite
l'intervention des brise-glace. En revanche la partie orientale de la Mer
de Chine Méridionale est réchauffée toute l'année
par le courant chaud du Kuroshio qui amène les eaux à une
température proche de 26°C [Su and Weng, 1994]. L’ensemble
des deux mers apparaît donc comme étant un test sévère
pour la modélisation des marées océaniques.
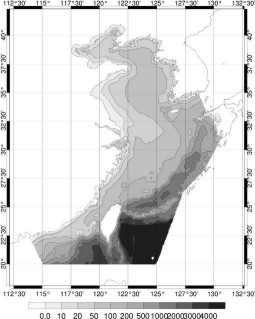
Figure 67 : Bathymétrie de la
zone d’étude (profondeurs en mètres)
12.2.3 Choix d’une base de données
marégraphiques pour les comparaisons
Nous avons sélectionné 192 marégraphes.
Ces stations ont été extraites de la banque de données
du Bureau Hydrographique International [International Hydrographic Office,
1979] et d’un rapport Coréen (Yoon, communication personnelle,
1995). Pour constituer notre propre banque de données, nous avons
contrôlé une à une celles des banques BHI et coréenne
dans notre zone afin de déterminer leur validité. Nous avons
du ajuster les données des marégraphes de l’étude
coréenne au méridien de Greenwich car elles étaient
référencées par rapport à la longitude 135°E.
A partir de ces données nous nous
sommes donc constitué notre propre banque de données suivant
plusieurs critères :
-
Localisation : si les coordonnées d'un marégraphe étaient
en pleine terre, il était écarté (soit il était
placé dans un estuaire, soit les coordonnées étaient
fausses).
-
Cohérence spatiale : si un marégraphe n'était pas
cohérent, soit en amplitude, soit en phase, avec des marégraphes
environnants ( en dehors des zones de points amphidromiques) il était
écarté.
-
Temps de mesure : si le temps de mesure d'un marégraphe était
trop court (en général inférieur à un mois
afin de séparer correctement M2 des autres ondes
dans le spectre), il était écarté.
-
Doute sur la provenance de la donnée marégraphique : si une
donnée était fournie sans date, ni temps de mesure, elle
était écartée.
Les marégraphes pris en compte dans
cette étude sont donnés Figure 66. Nous pouvons tout de suite
constater que les mesures marégraphiques sont essentiellement côtières.
Les données pélagiques sont rares et la validation du modèle
en plein océan est donc plus hasardeuse. Cependant, le modèle
se comporte de manière connue en plein océan et ce sont les
zones côtières qui nous intéressent plus particulièrement.
Afin de comparer les solutions de marées
calculées avec les mesures in situ, nous introduisons une Root Mean
Square (RMS) :
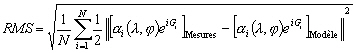 (12.133)
(12.133)
avec :
-
 la norme telle que pour un complexe
:
la norme telle que pour un complexe
: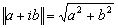 ;
;
-
N le nombre d’observations ;
-
i l’indice sur les observations ;
-
a i l’amplitude du point d’indice i ;
-
Gi la phase du point d’indice i.
Dans la suite du chapitre, toutes les comparaisons
seront faites avec cette RMS. Comme nos calculs sont purement hydrodynamiques
(aucune donnée n’est assimilée), les valeurs données
par les 192 stations marégraphiques sont indépendantes de
nos solutions ce qui assure des comparaisons cohérentes.
12.3 Etude de sensibilité
12.3.1 Choix de la zone d’étude
L’un des buts du travail sur ces mers littorales
est d’améliorer les solutions hydrodynamiques FES94. La zone modélisée
s’étend de la latitude 20°N à 40°N et de la longitude
113°E à 132°E. Le choix des conditions aux limites est très
important, surtout le long de frontières en plein océan où
la marée est nettement mieux connue qu’en petits fonds. La zone
suit des côtes de la Chine, de la Corée du Nord, de la Corée
du Sud et du Japon ainsi que des îles. Les frontières ouvertes
sont choisies en fonction de la bathymétrie, des mesures marégraphiques
disponibles et des zones de plein océan où les marées
issues des modèles globaux sont a priori bien connues. La détermination
de ces frontières ouvertes est absolument fondamentale car elle
conditionne une grande partie de la qualité des solutions calculées.
Dans la zone étudiée, FES94 est peut-être la meilleure
solution le long des côtes mais elle ne l’est pas en plein océan.
C’est pour cette raison que nous avons considéré deux modèles
globaux de marée pour définir les conditions aux limites
ouvertes : le modèle global CSR3.0 [Eanes and Bettadpur,
1996] et le modèle global FES95.2 [Le Provost et al., 1998].
Afin de comparer la qualité de ces deux modèles le long des
segments des frontières ouvertes choisies a priori (une première
simulation ne prenait pas en compte l’île de Taiwan en entier et
conduisait à des résultats médiocres) nous avons construit
une banque de données de 16 marégraphes localisés
près de ces segments. En utilisant la RMS introduite en (12.133),
le Tableau 32 donne les comparaisons de ces deux modèles avec les
mesures in situ.
|
Onde
|
Nombre de marégraphes
|
RMS pour CSR3.0 (cm)
|
RMS pour FES95.2 (cm)
|
|
M2
|
16
|
12,06
|
10,28
|
|
K1
|
14
|
2,03
|
2,85
|
Tableau 32 : RMS de CSR3.0 et FES95.2 le long des frontières
ouvertes
Le Tableau 32 montre que la solution FES95.2
est meilleure pour M2 (presque 2 cm de mieux que CSR3.0)
mais moins bon pour K1 (presque 0.8 cm moins bon que
CSR3.0). Un des buts de notre étude étant d’améliorer
notre modèle FES95.2 le long des côtes (puisqu’il est déjà
bon en plein océan) et comme il est difficile de départager
les deux modèles sélectionnés dans notre zone d’étude,
nous avons finalement opté pour FES95.2 pour fixer nos conditions
aux limites. Ainsi en incluant notre modèle local dans FES95.2 nous
améliorerons la solution globale FES95.
12.3.2 Mode de calcul
Comme nous l’avons vu précédemment,
le modèle original élément finis [Le Provost and
Poncet, 1978], suppose l’existence d’une unique onde dominante, en
terme de vitesse, dans la zone. Cependant, le long des côtes de l’océan
Arctique, Lyard [1997] a montré qu’il est important de relâcher
cette hypothèse au sein de zone où les vitesses des ondes
diurnes peuvent être équivalentes voire supérieures
à celles des ondes semi-diurnes. C’est pourquoi, afin de vérifier
cette hypothèse dans la zone YS-ECS, nous avons calculé la
solution M2 dans deux cas :
-
un cas où M2 est la seule onde supposée
dominante (mode dominant) ;
-
un cas où M2 est dominante dans une partie de
la zone et K1 dans l’autre partie (mode mixte).
Le mode mixte nous permet de tenir compte
tout à la fois de la dominance des ondes diurnes et des ondes semi-diurnes
pour la linéarisation du coefficient de frottement. Le Tableau 33
donne les RMS calculées pour les différents modes.
|
Mode
|
RMS (cm)
|
|
Mode dominant
|
123,29
|
|
Mode mixte
|
30,24
|
Tableau 33 : RMS pour le mode dominant et le mode mixte
De façon claire et surprenante,
le mode mixte est 4 fois plus précis que le mode dominant. La formulation
du coefficient de frottement dans le mode mixte est commandée à
la fois par les vitesses de M2 et de K1.
Ces deux composantes jouent le rôle d’ondes dominantes générant
de la turbulence dans la couche limite proche des fonds océaniques
(cf. [Lyard, 1999] pour plus d’explications). Ainsi dans la suite,
tous les calculs sont faits en mode mixte.
12.3.3 Test sur la résolution
du maillage
Pour les calculs globaux FES, les équations
de l’hydrodynamique sont résolues sur un maillage de plus de 300000
nœuds. Cependant sur la zone YS-ECS la résolution de ce maillage
global n’est que de d’environ 10000 nœuds, ce qui représente des
tailles de mailles de 200 km en plein océan qui approchent les 10
km le long des côtes (Figure 68). Cette résolution est faible
pour l’étude locale approfondie que nous désirons réaliser.
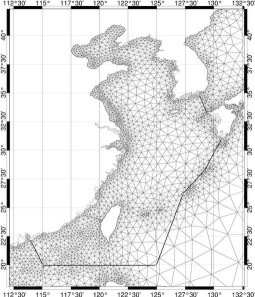
Figure 68 : Maillage global sur la
zone YS-ECS
En fonction de l’approche éléments
finis, nous avons remaillé notre zone afin d’améliorer les
performances du modèle hydrodynamique global dans cette zone. Ce
raffinement du maillage permet une meilleure prise en considération
de la topographie locale. Ainsi, comme nous l’avons vu dans précédemment,
Le
Provost et Vincent [1986] ont fixé la distance maximale 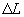 entre
deux nœuds nœuds Lagrange P2 d’un élément triangulaire pour
une simulation correcte de la propagation d’une onde de marée :
entre
deux nœuds nœuds Lagrange P2 d’un élément triangulaire pour
une simulation correcte de la propagation d’une onde de marée :
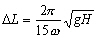 (12.134)
(12.134)
Par exemple pour l’onde M2
(choisie comme référence pour notre maillage) et une profondeur
de 1000 m, la distance maximale entre deux nœuds est d’environ 150 km.
Cependant ce critère n’est pas suffisant
dans les zones maritimes de forts gradients topographiques [Luettich
and Westerink, 1995]. Nous avons donc généré notre
nouveau maillage en tenant compte d’un critère supplémentaire
sur le gradient 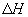 de la topographie
à un point de profondeur H. La distance maximale
de la topographie
à un point de profondeur H. La distance maximale 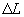 entre deux nœuds d’un élément triangulaire Lagrange P2 ne
doit pas exéder :
entre deux nœuds d’un élément triangulaire Lagrange P2 ne
doit pas exéder :
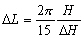 .
(12.135)
.
(12.135)
Ainsi, pour une profondeur de 1000 m et
une pente de fond de 1% la distance maximale entre deux nœuds est de 20
km environ.
Nous avons sélectionné le
meilleur de ces deux critères pour déterminer l’emplacement
de tous les nœuds du nouveau maillage (Figure 69).
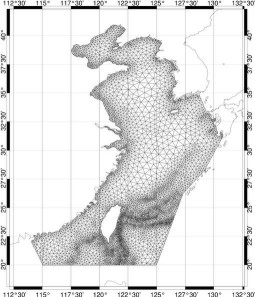
Figure 69 : Maillage raffiné
sur la zone YS-ECS
Comme nous pouvons le voir sur la Figure
68 et sur la Figure 69, la cassure de plateau entre la Mer Jaune et l’Océan
Pacifique est fortement marquée dans le maillage raffiné.
En effet, cette zone est à fort gradient topographique puisque les
profondeurs passent rapidement de 4000 m à une centaine de mètres
seulement. En termes pratiques, la distance entre deux nœuds P2 du maillage
raffiné est de 30 km environ en plein océan et de 5 km environ
le long des côtes. Ainsi, nos nouvelles solutions sont calculées
avec un maillage composé de 11448 triangles. Comme les calculs se
font avec une résolution en Lagrange P2, le nombres de nœuds est
de 23380. L’élévation de marée est calculée
en tous ces nœuds et les vitesses en tous les points de Gauss des éléments
triangulaires (7 pour chaque triangle).
Cependant, nous n’avons pas été
capables de quantifier les améliorations apportées après
avoir raffiné le maillage dans les mers marginales de la zone YS-ECS
à cause des effets intrinsèques sur l’amélioration
de la bathymétrie. La grille de bathymétrie à 5’x5’
(~ 10 km de résolution à l’équateur) ETOP05 [National
Geographic Data Center, 1987] est à la fois utilisée
pour le modèle local et le modèle global. Dans l’approche
par éléments finis, la bathymétrie est interpolée
sur tous les points de Gauss et est ainsi plus précise et plus dense
avec le maillage raffiné. Comme les solutions locales et les solutions
globales ne sont pas calculées avec la même bathymétrie,
les inter comparaisons des résultats numériques ne sont pas
significatives.
Cependant, il est évident que le
raffinement du maillage le long des côtes et en petits fonds permet
de mieux prendre en compte de petites structures comme les baies et les
estuaires, alors que le maillage global ne le fait pas. Ainsi, avec une
meilleure résolution spatiale, en particulier le long des côtes,
le maillage local représente mieux les gradients et les irrégularités
de la topographie.
12.3.4 Test sur la bathymétrie
et les autres champs de forçage
Les solutions de marées sont sensibles
à la topographie des fonds marins. En particulier, la bathymétrie
locale pilote la propagation des ondes. De plus, les forts gradients de
la topographie sont responsables des fortes variations des champs de vitesses.
Dans la Mer Jaune, et plus particulièrement dans la baie de Corée
et dans la baie de Pohai, la géométrie locale est à
l’origine des très fortes résonances d’ondes diurnes et semi-diurnes
le long des côtes. Ce résultat est confirmé par Kang
et al. [1998] qui ont analysé les fortes amplitudes de M2
dans la baie de Corée en terme de distorsion de l’onde de marée
sur les côtes coréennes. En outre, la précision et
la finesse de la topographie des fonds océaniques sont essentielles
pour une meilleure résolution de la dissipation de marée.
La bathymétrie utilisée dans CEFMO est extraite de la base
de données ETOP05.Cependant, les premières simulations étaient
différentes des données in situ. Smith [1993] a montré
un réel manque de précision de cette base de données.
Un des problèmes particuliers est du au fait que ETOP05 repose sur
l’analyse des échos sondages des navires. Les lignes de sondes sont
parfois distantes de plus d’une centaine de kilomètres. Or ETOP05
est interpolée entre ces lignes. C’est pourquoi, de nombreuses caractéristiques
de la topographie sous-marine présentes sur le terrain ne sont pas
représentées dans ETOP05. De plus, la résolution spatiale
de ETOP05 est insuffisante (la résolution numérique est de
5’x5’ ce qui est nettement supérieure à la résolution
du terrain) en particulier en petits fonds et le long des côtes.
Nous avons entrepris d’améliorer la bathymétrie ETOP05 dans
la zone YS-ECS en utilisant des cartes de la Marine Française et
de la Navy Anglaise. Dans certaines zones de petits fonds d’une trentaine
de mètres, nous avons constaté des différences supérieures
à 10 m. Puis nous avons calculé des solutions pour les ondes
M2et
K1 avec la bathymétrie ETOP05 et notre bathymétrie
améliorée. Les résultats des comparaisons avec la
base de données définies dans le paragraphe 12.2.3 sont donnés
dans le Tableau 34.
|
Onde
|
Nombre de marégraphes
|
RMS pour la bathymétrie ETOP05 (cm)
|
RMS pour la bathymétrie amélioré (cm)
|
Pourcentage d’amélioration
|
|
M2
|
192
|
44,82
|
28,58
|
36%
|
|
K1
|
171
|
10,04
|
7,01
|
30%
|
Tableau 34 : Comparaisons de la bathymétrie ETOP05 et de la
bathymétrie améliorée
Les résultats sont parlants. En
effet, les améliorations pour M2 sont de 36% et
pour K1 de 30%, ce qui met en évidence la réelle
importance de la bathymétrie dans la modélisation hydrodynamique.
Nous avons aussi tenu compte des marées
terrestres, des effets de charges et des effets d’auto-attraction. Hendershott
[1972] a exprimé les effets de charges et d’auto-attraction comme
nous l’avons vu dans le paragraphe 6.2. Des cartes globales ont été
calculées par Francis [1990], en prenant
pour base les solutions de marées de Schwiderski [1980c]
avec une résolution de 1ºx1º. Nous les avons introduit
comme termes diagnostiques dans notre modèle éléments
finis.
12.3.5 Réglage du coefficient
de frottement
Dans le modèle hydrodynamique CEFMO,
le coefficient de frottement est paramétrisé par une loi
quadratique. Ce coefficient Cf de type Chézy est
utilisé empiriquement pour ajuster le frottement. Il est habituellement
pris entre 2,5x10-3 et 3x10-3 [Dronkers, 1964].
En effectuant des expériences sur le plateau continental européen,
Pingree
[1987] recommande l’utilisation d’un coefficient compris entre 2,30x10-3
et 2,60x10-3. Pour la simulation de marée globale FES94.1,
Le
Provost et al. [1994] ont pris un coefficient de 3x10-3
dans les zones de plein océan et de 2,5x10-3 dans les
petits fonds. Jusqu’à maintenant ce coefficient déterminé
sur un domaine réduit était appliqué sur l’océan
global.
Des tests ont été entrepris
sur la zone YS-ECS avec 9 coefficients de frottement différents
(1x10-3, 1,25x10-3, 1,5x10-3, 1,75x10-3,
2x10-3, 2,25x10-3, 2,5x10-3, 2,75x10-3
et 3x10-3) afin de déterminer le meilleur par rapport
à notre base de données marégraphiques introduite
au paragraphe 12.2.3. Les tests ont révélé un effet
de seuil à 1,5x10-3 pour M2 et K1
(cf. Figure 70 et Figure 71).
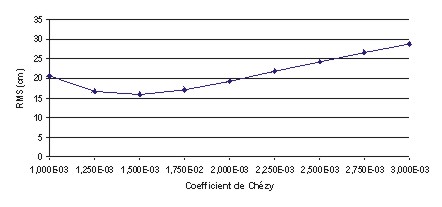
Figure 70 : RMS (en cm) des solutions
calculées pour M2 en fonction du coefficient de
frottement
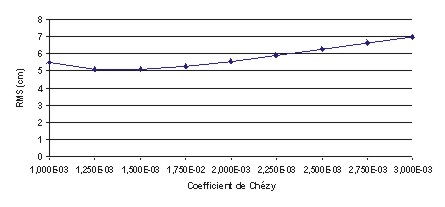
Figure 71 : RMS (en cm) des solutions
calculées pour K1 en fonction du coefficient de
frottement
L’amélioration est de 45,3% pour
M2
et de 27,2% pour K1 pour un coefficient de frottement
décroissant de 3x10-3 à 1,5x10-3. C’est
pourquoi, dans la suite du travail, le coefficient de frottement est pris
égal à 1,5x10-3 pour le calcul de toutes les ondes
de marées. Ceci confirme que le coefficient de frottement optimal
à une échelle régional peut-être différent
de celui de l’échelle globale.
12.4 Calcul de 11 ondes de marées
12.4.1 Décomposition harmonique
du spectre de marée
Onze ondes du spectre de marée ont
été calculées : M2, S2,
N2,
K2,
2N2, K1,
O1,
P1,
Q1, M4 et MS4. Ces
composantes ont été sélectionnées en fonction
de la décomposition harmonique du signal fourni par les 192 marégraphes
sélectionné au paragraphe 12.2.3. Nous avons calculé
une amplitude moyenne pour chacune des composantes (cf. Figure 72).
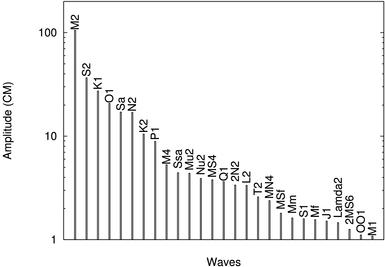
Figure 72 : Décomposition harmonique
du spectre de marée de la base de données in situ
Nous avons ainsi pu déterminer les
composantes principales du spectre sur la zone YS-ECS.
Comme nous étudions une zone principalement
située en petits fonds, les effets de la non-linéarité
des ondes de marée sont importants. Des ondes qui ne sont pas présentes
en plein océan apparaissent ainsi en petits fonds. C’est le cas
des deux ondes quart-diurnes M4 et MS4.
En effet, ces deux composantes résultent principalement du fait
que quand une vague arrive en eau peu profonde, le creux de la vague est
retardé par rapport à sa crête. Les ondes qui s’en
déduisent perdent leur aspect purement harmonique [Le Provost,
1991; Parker, 1991]. C’est pourquoi, nous avons aussi calculé
ces deux ondes non linéaires.
12.4.2 Représentation des ondes
La représentation en amplitude et en
phase des principales ondes est donnée dans Lefèvre et
al. [1999c]. Nous rappelons ci-dessous les résultats pour M2,
K1,
M4
et MS4.
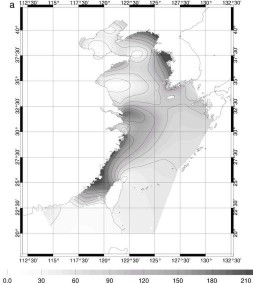
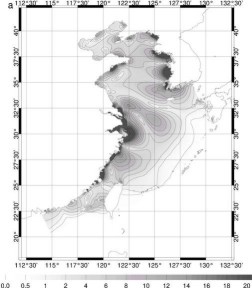
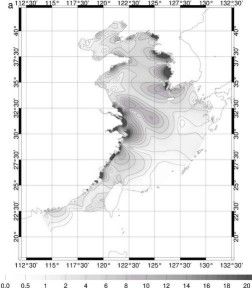
Figure 73 : Amplitude ((a) en cm)
et phase ((b) en degrés) de marées pour M2
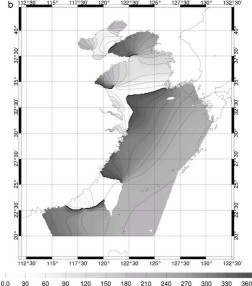
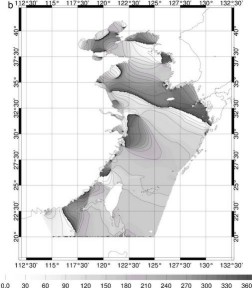
Figure 74 : Amplitude ((a) en cm)
et phase ((b) en degrés) de marées pour K1
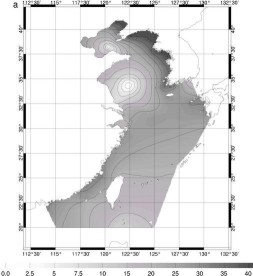
Figure 75 : Amplitude ((a) en cm)
et phase ((b) en degrés) de marées pour M4
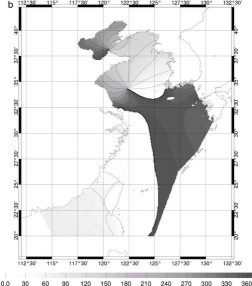
Figure 76 : Amplitude ((a) en cm)
et phase ((b) en degrés) de marées pour MS4
12.4.3 Qualité des ondes calculées
Le calcul des 11 ondes a été
effectué et comparé à d’autres solutions de marée
sur la Mer Jaune et les Mers de Chine Orientale. Ces comparaisons sont
amplement développées dans le papier de [Lefèvre
et al., 1999c]. Nous ne rappellerons donc que les résultats
quantitatifs de l’étude. Nous résumons la qualité
de nos 11 ondes calculées dans le Tableau 35.
|
Onde
|
Nombre de marégraphe
|
Variance sur les marégraphes en cm
|
RMS des solutions en cm
|
Pourcentage de précision
|
|
M2
|
189
|
87,06
|
15,82
|
96,70%
|
|
S2
|
189
|
30,39
|
13,15
|
81,26%
|
|
N2
|
20
|
14,44
|
5,86
|
83,53%
|
|
K2
|
33
|
8,75
|
2,04
|
94,59%
|
|
2N2
|
9
|
3,16
|
1,77
|
68,74%
|
|
K1
|
163
|
20,32
|
5,09
|
93,73%
|
|
O1
|
163
|
15,19
|
3,76
|
93,88%
|
|
P1
|
40
|
6,61
|
1,85
|
92,19%
|
|
Q1
|
163
|
2,67
|
0,70
|
93,22%
|
|
M4
|
15
|
6,01
|
5,74
|
62,15%
|
|
MS4
|
11
|
2,83
|
2,46
|
24,32%
|
Tableau 35 : Qualité des 11 ondes calculées
La première colonne du Tableau 35
donne le nom de l’onde considérée. La deuxième donne
le nombre de marégraphes utilisés pour les comparaisons suivant
l’onde. La troisième indique la RMS calculée pour les marégraphes.
La quatrième donne la RMS des solutions calculées. La dernière
représente un pourcentage de précision (POA= Percentage Of
Accuracy) qui est un bon indicateur de la qualité d’une solution
comparée à une banque de données in situ :
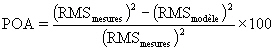 (12.136)
(12.136)
Ce pourcentage, nous permet d’exprimer
la qualité d’une solution pour une onde donnée en fonction
de notre banque de comparaison les unes par rapport aux autres. Le Tableau
35 montre que les principales composantes du groupe des semi-diurnes M2et
du groupe des diurnes K1 sont bien expliquées,
comparées aux données in situ. S2 et N2
sont moins bien expliquées que les autres ondes : ceci est très
certainement dû au fait que les conditions aux limites sont extraites
de la solution globale FES95. En effet, elles ne sont pas très bonne
qualité, en particulier à la frontière entre la Mer
Jaune et la Mer du Japon, ce qui affecte l’ensemble de la solution sur
tout le domaine local. Cependant, comme il a été écrit
précédemment, afin de garder la continuité entre FES95.2
et notre solution, nous avons conservé FES95.2 pour extraire nos
conditions aux limites ouvertes. En outre, il est à noter qu’exceptées
les quatre ondes principales M2, S2,
K1
et O1 les comparaisons entre les solutions calculées
et les mesures in situ, se font avec très peu de marégraphes.
Ceci biaise un peu l’analyse et les résultats de ces comparaisons,
en particulier pour les ondes non linéaires
M4
et MS4 qui, en général, ne sont pas bien
extraites du spectre de marée (erreurs significatives en phases
en particulier). Enfin, il est à souligner que ces deux composantes
ont des longueurs d’ondes plus courtes et nécessiteraient plus de
données in situ pour la validation.
12.5 Energie de marée
12.5.1 Vitesses barotropiques
Afin de calculer le bilan énergétique
des marées dans la zone YS-ECS, nous avons dû calculer les
vitesses barotropiques des composantes du spectre de marée. Les
résultats des calculs sont développés et comparés
dans Lefèvre et al. [1999c]. Nous donnons à titre
informatif les ellipses de courant pour les deux ondes principales, projetées
sur une grille régulière (Figure 77 et Figure 78). Le grand
axe (respectivement petit axe) représente le maximum (respectivement
minimum) de vitesse.
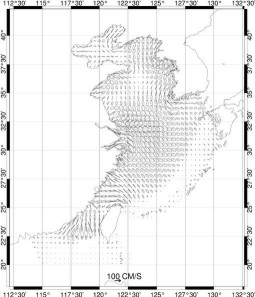
Figure 77 : Ellipses des vitesses pour
M2
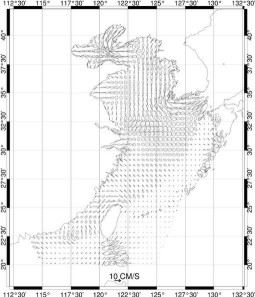
Figure 78 : Ellipses des vitesses pour
K1
Dans la Mer Jaune les vitesses M2
et K1 sont complémentaires comme le montre la
Figure 77 et la Figure 78. Or les vitesses sont représentatives
de la dissipation de marée. Nos calculs nous conduisent à
conclure que quand l’onde M2 pénètre dans
la zone YS-ECS, elle se dissipe principalement dans les petits fonds, alors
que l’onde K1 se dissipe surtout à l’entrée
de la Mer Jaune où l’Océan Pacifique se resserre et à
l’entrée de la baie de Liatong. Comme les deux ondes sont complémentaires
dans la zone étudiée, bien qu’elles aient jusqu’à
5 ordres de différence en norme de la vitesse, l’hypothèse
de dissipation mixe (mode mixte introduit au paragraphe 12.3.2) est à
nouveau confirmé.
12.5.2 Budget énergétique
de la marée
Nous avons quantifié la dissipation
globale de marée en fonction des variations du coefficient de frottement.
Comme nous l’avons conclu plus haut, une friction mixte est nécessaire
à la bonne modélisation de la marée dans la zone YS-ECS.
Ainsi, pour une onde considérée, le bilan global de l’énergie
de marée est la somme de :
-
l’énergie du forçage astronomique(contribution de la Lune
et du Soleil) ;
-
l’énergie des effets de charge et d’auto-attraction (perturbation
du potentiel astronomique) ;
-
la dissipation de l’onde considérée par rapport au coefficient
de frottement de l’onde dominante (M2 si l’onde calculée
est semi-diurne et K1 si elle est diurne) ;
-
la dissipation de cette onde par rapport au coefficient de frottement de
l’onde secondaire (K1 si l’onde calculée est semi-diurne
et M2 si elle diurne).
Ces bilans énergétiques ont
été calculés avec les vitesses de marée pour
les sept coefficients de frottement. Les valeurs numériques sont
données dans Lefèvre et al. [1999c]. De manière
surprenante, la dissipation reste constante, à la fois pour l’onde
M2
et l’onde K1, en fonction des variations du coefficient
de frottement. En outre la dissipation que nous avons calculée est
la même que celle calculée par Le Provost et Lyard
[1997] avec un modèle hydrodynamique global, bien que la topographie,
le maillage et le coefficient de frottement aient été améliorés.
La raison principale de cette constatation est que le champ de vitesse
s’adapte aux variations du coefficient de frottement du modèle hydrodynamique
pour dissiper la même quantité d’énergie fournie aux
frontières ouvertes qui sont fixées par les conditions aux
limites.
12.5.3 Sensibilité des champs
de vitesses
La constance de la dissipation, alors que
le coefficient de frottement varie, nous a amené à conduire
une étude de sensibilité sur les élévations
de marée et les vitesses de marée en fonction des variations
de ce coefficient. Lefèvre et al. [1999c] ont montré
que pour un coefficient de frottement variant de 1x10-3 à
3x10-3, les élévations de M2
décroissent de 16,5% et les vitesses d’environ 29% alors que la
dissipation due à la marée ne décroît que de
5,4% alors que le coefficient de frottement est multiplié par 3
(variation de 300% !). Les mêmes constatations sont faites pour K1.
Les vitesses de marée apparaissent comme étant deux fois
plus sensibles aux variations du coefficient de frottement que les élévations.
En théorie, l’expression (cf. [Le Provost and Lyard, 1997])
de la dissipation 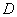 de marée
est :
de marée
est :
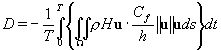 (12.137)
(12.137)
avec :
-
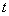 : le temps ;
: le temps ;
-
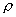 : la densité de l’eau ;
: la densité de l’eau ;
-
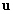 : la vitesse barotrope horizontale
;
: la vitesse barotrope horizontale
;
-
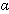 : l’élévation de surface
de l’océan ;
: l’élévation de surface
de l’océan ;
-
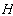 : la profondeur d’eau moyenne ;
: la profondeur d’eau moyenne ;
-
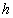 : la profondeur d’eau instantanée
(
: la profondeur d’eau instantanée
(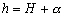 ) ;
) ;
-
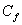 : le coefficient de friction sans
dimension de type Chézy.
: le coefficient de friction sans
dimension de type Chézy.
Nous pouvons reconnaître dans (12.137)
l’expression du frottement sur le fond océanique :
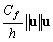
D’après (12.137), la dissipation
est proportionnelle au coefficient de frottement multiplié par le
cube de la vitesse de marée, ce qui est vérifié dans
le cas de notre zone d’étude [Lefèvre et al., 1999c].
Il est clair que les vitesses sont plus sensibles aux variations du coefficient
de frottement que ne le sont les amplitudes de marée. Une vérification
expérimentale avec des mesures in situ de courantomètres
a montré que les vitesses calculées correspondent le mieux
aux vitesses mesurées dans le cas du choix d’un coefficient de frottement
égal à 1.5x10-3, ce qui confirme l’étude
faite précédemment sur les amplitudes. Le Tableau 36 donne
les bilans énergétiques déduits de ces calculs de
vitesses.
|
Onde
|
Bilan énergétique (GW)
|
|
M2
|
-180,2
|
|
K1
|
-11,2
|
|
S2
|
-59,9
|
|
N2
|
-16,4
|
|
K2
|
-3,3
|
|
2N2
|
-0,3
|
|
O1
|
-6,0
|
|
P1
|
-1,0
|
|
Q1
|
-0,2
|
Tableau 36 : Bilan énergétique pour les ondes principales
du spectre de marée et un coefficient de frottement optimisé
12.6 Apports de l’étude locale
Grâce à l’étude de la
modélisation des marées par notre modèle hydrodynamique
local, nous avons été à même de dégager
les principales améliorations à apporter au modèle
global FES pour obtenir de meilleures solutions de marée en zone
littorale. Par la comparaison avec une base de données marégraphiques
conséquente, nous avons pu quantifier ces apports. Les améliorations
constatées s’expliquent par 5 points :
-
le choix d’un mode mixte de calcul qui prend à la fois en compte
la dominance des vitesses de M2 dans certaines parties
de la zone YS-ECS et celle de K1 dans les autres parties
;
-
un raffinement important du maillage éléments finis en particulier
en petits fonds et sur les gradients de topographie ;
-
le choix de conditions aux limites issues du modèle global FES95.2
de bonne qualité en plein océan ;
-
une topographie raffinée (amélioration de 36% pour M2
et de 30% pour K1) ;
-
l’utilisation d’un coefficient de frottement spécifique (amélioration
de 45.2% pour M2 comparé à la valeur classique
de 3x10-3).
Les ondes M2,, S2,
N2,
K2,
et 2N2 (pour le groupe des semi-diurnes), K1,
O1,
P1, et Q1
(pour le groupe des diurnes) ont été calculées
en bénéficiant des améliorations citées ci-dessus.
De plus, les ondes non linéaires M4 et MS4
(pour les groupes des quart-diurnes) ont été calculées
et comparées à d’autres modèles locaux, avec succès.
Ceci montre la capacité du modèle CEFMO à calculer
des ondes non linéaires.
Les champs de vitesses associés
aux neuf ondes diurnes et semi-diurnes ont aussi été calculés
afin de faire un bilan énergétique précis de la marée
dans la zone YS-ECS en fonction des variations du coefficient de frottement.
La dissipation calculée reste alors constante ce qui montre que
son expression théorique est consistante. La principale conclusion
sur cette constance de la dissipation est que dans le cadre de notre modèle
hydrodynamique, le champ de vitesse d’adapte aux variations du coefficient
de frottement.
Les améliorations que nous avons
apporté au modèle hydrodynamique local vont ainsi pouvoir
profiter au modèle global dans notre approche éléments
finis.
Partie IV : Bilan énergétique
et perspectives
Back | Next
Title: Thèse de Fabien Lefèvre
Issue: Version 1.0
Date: 29/09/2000



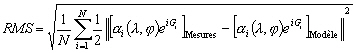 (12.133)
(12.133)
 la norme telle que pour un complexe
:
la norme telle que pour un complexe
: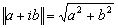 ;
;
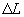 entre
deux nœuds nœuds Lagrange P2 d’un élément triangulaire pour
une simulation correcte de la propagation d’une onde de marée :
entre
deux nœuds nœuds Lagrange P2 d’un élément triangulaire pour
une simulation correcte de la propagation d’une onde de marée :
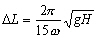 (12.134)
(12.134)
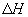 de la topographie
à un point de profondeur H. La distance maximale
de la topographie
à un point de profondeur H. La distance maximale 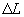 entre deux nœuds d’un élément triangulaire Lagrange P2 ne
doit pas exéder :
entre deux nœuds d’un élément triangulaire Lagrange P2 ne
doit pas exéder :
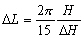 .
(12.135)
.
(12.135)





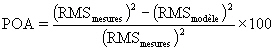 (12.136)
(12.136)


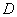 de marée
est :
de marée
est :
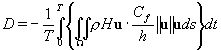 (12.137)
(12.137)
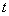 : le temps ;
: le temps ;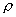 : la densité de l’eau ;
: la densité de l’eau ;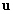 : la vitesse barotrope horizontale
;
: la vitesse barotrope horizontale
;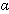 : l’élévation de surface
de l’océan ;
: l’élévation de surface
de l’océan ;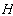 : la profondeur d’eau moyenne ;
: la profondeur d’eau moyenne ;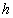 : la profondeur d’eau instantanée
(
: la profondeur d’eau instantanée
(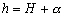 ) ;
) ;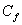 : le coefficient de friction sans
dimension de type Chézy.
: le coefficient de friction sans
dimension de type Chézy.