Figure 79 : Découpage en 35
zones pour le calcul de la nouvelle bathymétrie
§ bonne bathymétrie en zones pélagiques afin de mieux modéliser les échanges océaniques de grandes longueurs d’ondes ;
§ bathymétrie très précise sur les plateaux continentaux et en petits fonds car de nombreuses ondes de marée y prennent naissance (ondes non linéaires) ;
§ bons positionnement des forts gradients de bathymétrie afin de mieux tenir compte de la génération des ondes internes ;
§ bonne bathymétrie en zones polaires car peu de bathymétries de ces zones sont disponibles et validées ;
§ bons positionnement des côtes car étant très précis, ils permettent d’ajuster les petits fonds au mieux.
C’est pourquoi la compilation de diverses bases de données est nécessaire.
Diverses zones ont ainsi été obtenues :
Une zone de calcul est choisie. Elle correspond en général aux points de sondes disponibles et provenant d’une même origine. Le calcul de la bathymétrie a été divisée en 35 zones (Figure 79) qui prennent en compte à la fois les zones océaniques et les possibilités de calcul des ordinateurs.
Figure 79 : Découpage en 35
zones pour le calcul de la nouvelle bathymétrie
Chaque zone a été subdivisée en petits domaines de 5°x5° (voire plus petits encore si le nombre de points de sondes à interpoler était très important) afin d’être en accord avec la puissance de calcul informatique disponible.
Sur cette zone sont extraits tous les points de sondes de la base de données WVS qui correspondent à des profondeurs nulles. Ces points, très nombreux sont interpolés sur une grille de 0,5 x0,5° (supérieure à la précision de la base de données mais inférieure au pas de grille souhaité pour la bathymétrie mondiale).
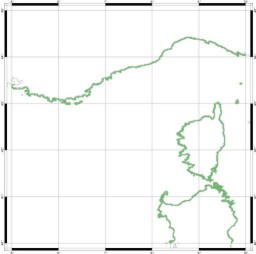
Figure 80 : Points de sondes côtiers
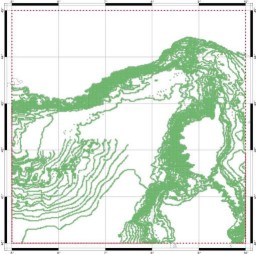
Puis sont extraits tous les points de sondes disponibles dans toutes les autres bases de données disponibles sauf ETOPO5, DBDB5 et Smith&Sandwell. Ces points sont eux aussi interpolés sur une grille 0,5’x0,5’.
Figure 81 : Points de sondes côtiers,
des isobathes et des bases de données personnelles
Ensuite le contour de la zone est déterminé pour compléter les points de sondes par des bathymétries mondiales.
DBDB5 est de bonne qualité le long des côtes, Smith&Sandwell est de bonne qualité en plein océan, donc pour compléter l’information des points de sondes définis précédemment, DBDB5 est utilisée de 0 à 200m, une interpolation linéaire entre DBDB5 et Smith&Sandwell est calculée entre 200 et 500m et Smith&Sandwell complète les fonds en dessous de 500m.
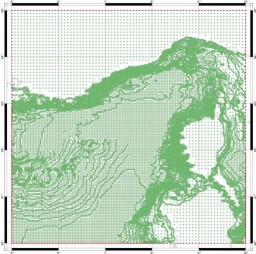
Figure 83 : Ensemble des points de
sondes utilisés pour l’interpolation
Pour toutes les zones ou Smith&Sandwell n’est pas définie, ETOPO5 est utilisée. Pour les fonds océaniques, les points ajoutés sont interpolés sur une grille de 2’x2’. Pour les terres, une interpolation de 4’x4’ est suffisante. En effet après l’interpolation, toutes les élévations des terres émergées seront recopiées de la base de données Swith&Sandwell interpolée à 2’x2’ et qui est très précise. Ensuite, afin de réaliser l’interpolation linéaire de tous ces points de sondes, un maillage éléments finis est calculé. L’utilisation des éléments finis est très avantageuse dans notre cas car elle nous permet de tenir compte de la position exacte des points de sondes. En effet, si nous avions travaillé en différences finies nous aurions deux possibilités. Il aurait fallu prendre un pas de grille tellement petit pour ne pas perdre la précision de positionnement de ces points de sondes que nous aurions largement dépassé la puissance de calcul des ordinateurs à notre disposition (en l’occurrence deux stations Sun UltraSparc 1 cadencée à 177MHz avec 256 Mo de mémoire vive). Ou bien nous aurions du interpoler la position des points de sondes sur des points espacés d’une grille différences finies et nous aurions perdu l’information exacte apportée par chaque point de sonde.
Figure 84 : Maillage des points de
sondes pour l’interpolation
Enfin, de ce maillage, une nouvelle bathymétrie a été interpolée linéairement Elle tient compte de la position réelle de tous les points de sondes, sur une grille 2’x2’.
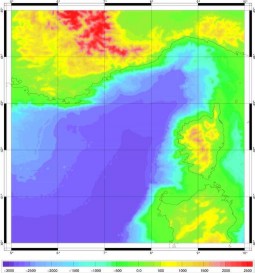
Figure 85 : Nouvelle bathymétrie
interpolée (profondeurs et altitudes en mètres)
Ainsi toutes les zones de 5°x5° sont calculées indépendamment puis elles sont assemblées en une bathymétrie mondiale. La continuité aux frontières des différentes zones est assurée car elles sont absolument identiques pour toutes les zones jointives.
Dans les zones polaires, Smith&Sandwell n’étant pas définie, ETOPO5 a été utilisée. Afin d’assurer une continuité entre les deux bathymétrie mondiales, une interpolation linéaire a été calculée entre –68° (Nord et Sud) et 72° (Nord et Sud).
Les maillages aux éléments finis des solutions FES antérieures étaient contraints par un critère basé sur la longueur d’onde théorique des ondes de marée de fréquence semi-diurne. Ils ne tenaient malheureusement pas compte de l’existence sur les pentes de la topographie d’ondes à plus courte échelle. Ils étaient également mal adaptés, sur ces même pentes, à la détermination précise des vitesses barotropes. Ils étaient sous-résolus pour les ondes quart-diurne. Du fait de la connaissance a priori que nous avons maintenant de la marée dans les bandes longues périodes, diurne, semi-diurne et bientôt quart-diurne, nous avons les moyens de corriger ce sous échantillonnage spatial en remaillant les domaines de modélisation. Par ailleurs, nous profiterons de cette remise à plat pour compléter notre modèle avec les mers adjacentes non incluses jusqu’à présent (Mer rouge, Golf Persique, Mer Noire...).
Nous présentons dans la suite la construction et les caractéristiques adaptées à l’usage spécifique des modèles de marée FES.
§ Le plateau Européen ;
§ Le plateau de Patagonie ;
§ La baie d’Hudson ;
§ La Mer du Labrador
§ La zone de la Malaisie ;
§ La Mer Jaune et les Mers de Chine ;
Ces régions à forte dissipation sont étroitement corrélées avec les petits fonds océaniques. Elles nécessitent donc une résolution de maillage plus importante afin de mieux déterminer dénivellation et vitesses.
En outre des zones de petits fonds avec des bathymétries approximatives se trouvent dans les zones polaires :
§ L’Océan arctique proche des côtes ;
§ La Mer de Ross ;
§ La Mer de Weddell.
Le rôle fondamental joué par les phénomènes non-linéaires dans la dynamique de la marée (ainsi que le regain d’intérêt pour l’océanographie côtière) et la nécessité de bien représenter ces phénomènes nous imposent d’étudier avec une résolution plus importante que de coutume les zones citées précédemment. L’approche multi bassins de notre modèle s’adapte particulièrement bien à une définition hétérogène de la résolution des maillages en zones peu profondes. Les régions citées précédemment ont été détachées du modèle de bassin dans lequel elles étaient incluses auparavant, pour constituer un modèle indépendant qui sera au final traité de façon analogue aux modèles de bassins océaniques dans l’algorithme de résolution globale.
Afin de mieux modéliser la marée, le nouveau maillage est fortement raffiné suivant les trois critères présentés ci-dessous.
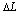pour le côté d’un triangle afin d’obtenir une simulation correcte
de la propagation d’une onde de marée à une valeur inférieure
à :
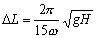(13.138)
:
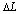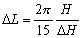(13.139)
La bathymétrie utilisée dans le calcul de ce critère est issue de ETOPO5 et a été améliorée en petits fonds.
La triangulation de Delaunay d’un ensemble de points est la triangulation de cet ensemble qui respecte la propriété stipulant qu’aucun point dans cet ensemble ne se trouve dans le cercle extérieur de tous les triangles de la triangulation. Ce cercle extérieur est le cercle qui passe par les trois sommets d’un élément triangulaire.
L’algorithme de Ruppert est peut être le premier algorithme de génération de maillages éléments finis qui fonctionne en pratique. Il génère des maillages sans angles trop petits en utilisant relativement peu de triangles (puisque la densité de triangle peut-être ajusté par l’utilisateur) et permet à la densité de triangle de varier rapidement sur de courtes distances.
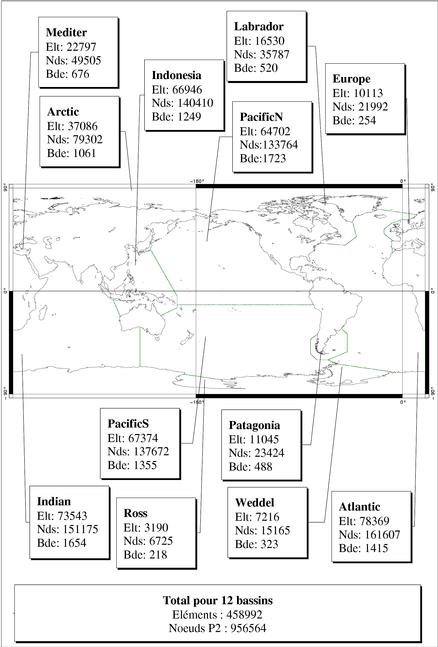
Figure 86 : Caractéristiques
des maillages
La Figure 86 indique le nombre d’éléments
triangulaires, le nombre de nœuds Lagrange P2 et la largeur de bande qui
composent chaque maillage éléments finis.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 37 : Caractéristiques des 12 maillages couvrant l’océan global
La taille du tmpdir est la taille du fichier qui doit être écrit sur disque dur au cours de la factorisation d’une matrice intermédiaire dans le code CEFMO calculant les solutions FES. Sa taille étant conséquente, elle conditionne les ressources nécessaires des machines de calculs. Elle est égale à :
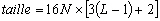(13.140)
avec :
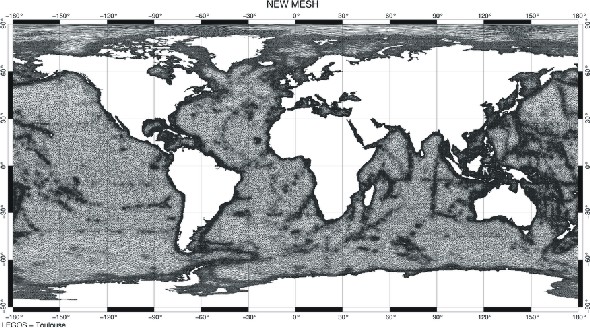
Figure 87 : Nouveau maillage éléments
finis global
Nous donnons pour information, les caractéristiques de ce supercalculateur utilisé dans le cadre de notre modélisation hydrodynamique.
Figure 88 : Processus itératif
simplifié du code CEFMO
Avec l’ancien maillage 6 itérations assuraient la convergence. Avec le nouveau maillage, nous avons fait des tests de convergence pour les ondes M2 et K1 afin de déterminer le nombre d’itérations nécessaires à la convergence. Ces solutions ont été calculées en mode forcé, c’est-à-dire que nous avons calculé les 12 bassins océaniques introduits dans le paragraphe 13.4.1.2, indépendamment les uns des autres. Les conditions aux limites sur les frontières fermées sont un flux nul Sur les frontières ouvertes, nous avons imposé des conditions aux limites en dénivellation extraites de la solution FES99. Imposer ces conditions aux limites nous permet de converger beaucoup plus vite vers un état stationnaire au cours du processus itératif. De plus, comme nous l’a montré l’étude locale du chapitre précédent, nous avons calculé nos solutions en mode mixte qui est plus proche de la réalité des phénomènes dissipatifs de la marée. Le mode mixte nous permet de tenir compte tout à la fois de la dominance des ondes diurnes et des ondes semi-diurnes pour la linéarisation du coefficient de frottement (M2 est dominante dans certaines zones de l’océan mondial et K1 dans les autres). En effet, nous avons vu par exemple que les marées à Dumont d’Urville sont diurnes (cf. mesures de ROSAME). Les marées semi-diurnes ne sont pas dominantes partout à la surface de la Terre. Afin de pouvoir quantifier ces itérations, nous avons comparé nos sorties de calculs avec la base de données ST95 composée de 95 données marégraphiques pélagiques (Figure 89 et Figure 90) et la base Topex composée de données altimétriques dans des fonds de plus de 200 m(Figure 91 et Figure 92).
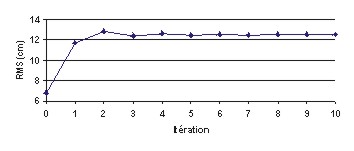
Figure 89 : RMS (en cm) des solutions
calculées pour M2 par rapport à ST95 en
fonction du nombre d’itérations
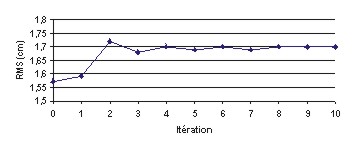
Figure 90 : RMS (en cm) des solutions
calculées pour K1 par rapport à ST95 en
fonction du nombre d’itérations
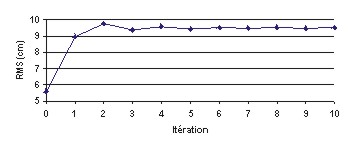
Figure 91 : RMS (en cm) des solutions
calculées pour M2 par rapport à la base
Topex en fonction du nombre d’itérations
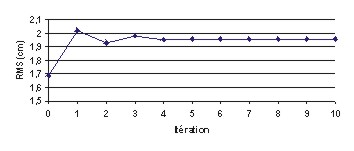
Figure 92 : RMS (en cm) des solutions
calculées pour K1 par rapport à la base
Topex en fonction du nombre d’itérations
Ces 4 figures nous montrent que nous avons la convergence assurée des solutions FES2000 en mode mixte forcé pour le nouveau maillage globalement atteinte en 10 itérations. Tous nos calculs en mode forcé avec le nouveau maillage nécessitent donc 10 itérations. Le saut de RMS que nous pouvons constater entre l’itération 0 et l’itération 1 s’explique par le fait que pour initialiser notre processus itératif, nous imposons initialement des vitesses arbitraires de 2 m.s-1 qui sont valables en milieu côtier, mais bien trop fortes en plein océan (plutôt de l’ordre du cm.s-1), il faut donc une à deux itérations supplémentaires pour obtenir un champ de vitesses de nature plus physique aussi bien en petits fonds qu’en plein océan.
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 38 : Comparaison des solutions libres avec ST95 et la base de données Topex
Comme nous pouvons le voir, nous sommes loin des précisions des solutions actuelles telles FES99. Sachant que la RMS sur les données de ST95 est de 33,5 cm (11,1 cm) la comparaison de notre nouvelle solution libre M2 (K1) avec ST95 représente un écart aux observations d’environ 33% (16%). Avec la solution assimilée FES99, il est de 4% (10%)
Si nous considérons les données de la base Topex, la RMS sur les données est de 26,1 cm (10,5 cm) et donc la comparaison de la solution libre M2 (K1) avec ces données est d’environ 47% (17%). Avec la solution assimilée FES99, elle est de 3% (9%). La Figure 93 présente la différence complexe entre la solution libre FES2000 et la solution FES99 pour l’onde M2. Globalement en plein océan, nous constatons des différences de l’ordre de plusieurs centimètres. Mais, dans la Mer du Labrador, la Mer de Weddell, la Mer de Tasmanie, le détroit de Béring, sur les plateaux Européens et Patagonien, ces différences atteignent 50 cm. Après une étude sur les phases, nous avons constaté que les différences en phases étaient minimes : elles sont donc principalement dues aux amplitudes de marées. Nous avons tracé Figure 94, la différence en amplitude pour l’onde M2 de la solution FES2000 moins la solution FES99, ce qui nous permet de déterminer les différences relatives de FES2000 par rapport à un modèle de marée en accord avec les mesures in situ. Sur la majeure partie de l’océan mondial, la nouvelle solution libre en dénivellation est plus élevée que la solution validée FES99 (à part le détroit de Madagascar la Mer de Timor et le plateau de Patagonie). Nous pouvons donc soupçonner un manque de dissipation dans notre modèle. Nous verrons plus loin que cette hypothèse est confirmée par un bilan énergétique de la marée.
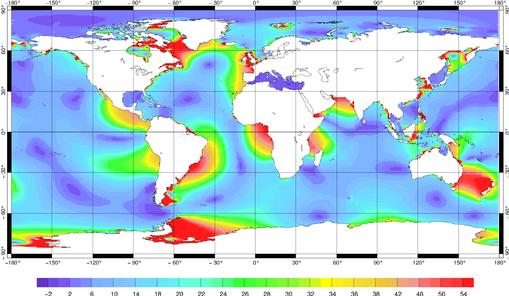
Figure 93 : Comparaison complexe pour
M2
de la solution FES2000 et de la solution FES99 (différences en cm)
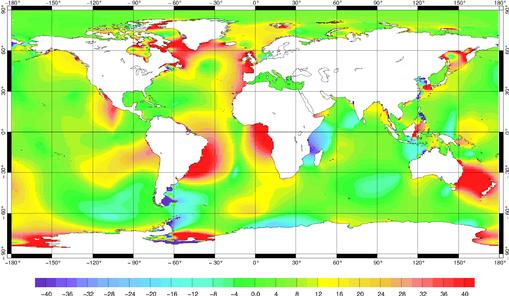
Figure 94 : Différence en amplitude
pour M2 de la solution FES2000 et de la solution FES99
(différences en cm)
De même que pour l’onde M2, la Figure 95 présente la différence en amplitude de la solution libre FES2000 moins la solution FES99 pour l’onde K1. Les différences sont moins marquées que pour M2. Si, majoritairement, l’amplitude de FES2000 est plus élevée dans le Pacifique et une grande partie de l’Indien, ce n’est pas le cas dans l’Atlantique Nord. Pour K1, nous n’avons pas comme pour M2 une amplitude uniformément trop forte de FES2000 par rapport à FES99.
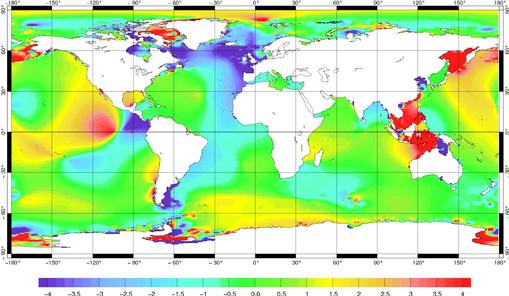
Figure 95 : Différence en amplitude
pour K1 de la solution FES2000 et de la solution FES99
(différences en cm)
Nous constatons le même phénomène que pour les solutions libres de FES98 et FES99 : la comparaison des nouvelles solutions libres n’est pas en bon accord avec les données de terrain et les modèles validés de marées. Nous pouvons soupçonner notre modèle de faire des approximations trop restrictives quant à la représentation physique du phénomène des marées. Par exemple, CEFMO ne modélise que les ondes de marées barotropes et ne tient pas compte des ondes baroclines. Il manque donc au moins une paramétrisation dans notre résolution. Le processus itératif présenté Figure 88 montre bien que le calcul des dénivellations de marée est issu du calcul des vitesses des marées et donc des coefficients de frottement que nous avons sur le fond des régions océaniques. Il est donc légitime de penser que si nous avons un problème de paramétrisation dans la résolution de nos équations, il faut regarder de près les vitesses et plus particulièrement le frottement qui est la base même de la physique de la marée océanique. Nous allons tenter d’identifier ce manque par une étude du bilan énergétique des marées issues de nos nouvelles solutions libres FES dans le paragraphe suivant. En effet, nous nous permettons de le rappeler, le but ultime des études en cours au LEGOS sur ces nouvelles solution FES est d’obtenir une solution de marée sans introduire d’information de mesures de terrain, donc sans condition aux limites ouvertes et sans assimilation de données.
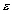par unité de surface d’une colonne d’eau élémentaire
est donnée par :
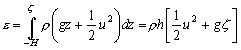(13.141)
avec :
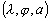: les coordonnées géocentriques
avec a le rayon de la Terre ;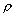
: la densité de l’eau de
mer ;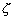
: la coordonnée verticale
;
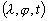: l’élévation
de la surface océanique ;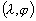
: la profondeur d’eau moyenne
;
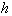
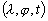: la profondeur d’eau instantanée (
)
;
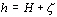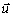
: la vitesse barotropique horizontale ;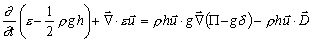
(13.142)
avec :
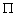: le potentiel global de la marée
(astronomique + effets de charge + auto-attraction) ;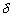
: l’élévation des
fonds océaniques dus aux marées terrestres et aux effets
de charges ;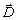
: la force de frottement sur les
couche limite du fond océanique.En intégrant sur un espace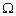 
délimité par ces frontières 
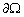et en moyennant sur une période T, nous obtenons :
F = P + D (13.143)
avec :
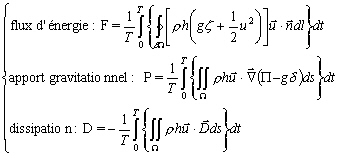(13.144)
Due à la périodicité des marées, seuls les termes intégraux pairs sont non-nuls :
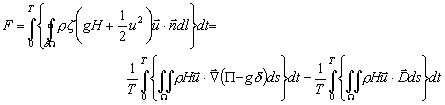(13.145)
Ainsi, le flux d’énergie au travers
des frontières ouvertes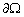 
du domaine océanique 
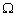doit correspondre au travail fourni par le forçage astronomique
et l’élévation de la surface des océans due à
la marée moins la dissipation.
est paramétrisé au moyen d’un coefficient adimensionnel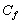 
de
type Chézy par la relation :
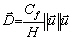(13.146)
La forme non-linéaire et non analytique nous pose un problème car nous ne pouvons pas adopter une approche linéaire pour le calcul des bilans énergétiques. En effet le spectre de marée est composé d’un très grand nombre d’ondes périodiques qui interagissent entre elles. Comme nous l’avons vu précédemment, dans le cadre de CEFMO, le coefficient de frottement est quasi linéarisé grâce à la supposition d’une onde dominante (cf. [Le Provost and Lyard, 1997] pour plus de détails). Pour chaque onde d’indice k, le frottement s’écrit sous la forme :
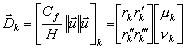(13.147)
avec :
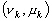les composantes sud-nord et ouest-est
complexes de la vitesse de la composante
k ;Cependant Le Provost et Lyard [1997] ont montré que l’onde M2 n’est pas dominante partout (du point de vu des vitesses). L’onde K1 est plus importante dans certaines zones (Mer d’Okhotsk, plateau de Sunda en Malaise et quelques zones autour de l’Antarctique). C’est pourquoi, le coefficient de frottement utilisé pour nos calculs est plus complexe car il prend en compte les effets de M2 et de K1 simultanément. Le frottement est ainsi évalué par :
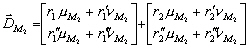(13.148)
sachant que :
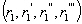sont les coefficients de frottement
calculé à partir des champs de vitesses de M2
en supposant que M2 est dominante.
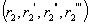sont les coefficients de frottement
calculé à partir des champs de vitesses de K1
en supposant que M2 n’est pas dominante.Ainsi, pour l’onde M2, l’énergie dissipée par le frottement de fond est la somme de deux termes :
D = D1 + D2 (13.149)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 39 : Bilan d’énergie de la solution libre M2 (énergie en Giga watts)
Comparons ces résultats avec ceux
obtenus par Le Provost et Lyard [1997] grâce aux champs de
vitesses calculés avec FES94.1 pour les grands bassins océaniques
:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 40 : Bilan énergétique obtenus par Le Provost et Lyard pour M2 avec le modèle FES94.1
Il faut noter que nos bassins et ceux de
Le
Provost et Lyard ne sont pas rigoureusement identiques (cf. surfaces)
car les maillages utilisés pour calculer FES94.1 et FES2000 sont
différents. C’est pourquoi, nous avons essayé dans la mesure
du possible de reconstruire les quatre principaux bassins entre les deux
solutions en sommant les bilans énergétiques. Nous avons
obtenu les quatre bassins suivants : Arctique, Atlantique, Indien et Pacifique.
Afin de quantifier les différences entre les énergies, nous
avons calculé les rapports de l’apport énergétique
et de la dissipation déduites des vitesses de FES2000 avec ceux
calculés à partir de FES94.1 sur les quatre bassins (Tableau
41).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 41 : Rapport des bilans énergétiques des solutions libres de FES2000 par rapport aux solutions de FES94.1
Les résultats du Tableau 41 sont assez difficiles à interpréter car les zones de comparaisons entre FES94.1 et FES2000 ne sont pas rigoureusement identiques. Cependant, il ressort que pour trois des quatre bassins (Arctique, Atlantique et Pacifique) les apports astronomiques et les dissipations calculées avec les solutions FES2000 sont plus élevées que pour celles calculées avec FES94.1. La dissipation obtenue avec FES94.1 a été validée par d’autres travaux indépendants [Church et al., 2000; Egbert, 1997; Kantha et al., 1995; Munk, 1997]. C’est donc la dissipation obtenue avec les solutions libres FES2000 qui est trop forte (3579,5 GW ce qui est environ 78% trop fort comparé aux 2010 GW obtenus avec FES94.1). Cette constatation est confirmée par notre étude sur les amplitudes de FES2000 (paragraphe 13.5.3) qui nous a montré que les amplitudes de marées sont trop fortes et donc que le phénomène dissipatif est trop faible. Nous savons que la dissipation est proportionnelle au cube de la vitesse. Les vitesses obtenues avec FES2000 sont donc trop fortes, ce qui conduit à penser que les coefficients de frottement qui sont introduit dans le calcul itératif de CEFMO sont trop faibles. Sous forme tensorielle, les coefficients de frottement pour l’onde M2 s’écrivent sous la forme de (13.147). Les coefficients r, r’, r’’ et r’’’ sont des fonctions de R et R’ (deux termes introduits dans la Partie 1 de cette thèse) dans les équations quasi-linéarisées [Le Provost and Vincent, 1986]. Dans le cas de l’onde dominante M2 nous avons :
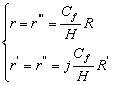(13.150)
Pour avoir un ordre d’idée de la distribution des coefficients de frottements issus de notre code de calcul, nous avons tracé les valeurs de R et R’ après 10 itérations du code CEFMO pour l’onde M2 (Figure 96 et Figure 97).
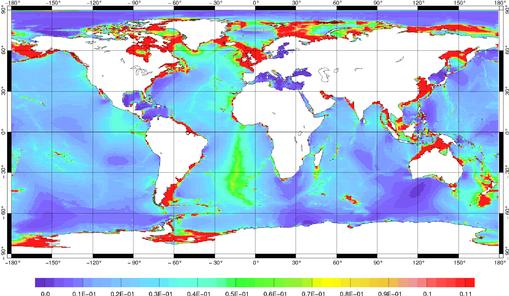
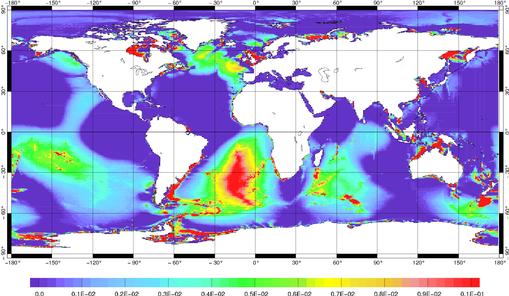
Figure 97 : Coefficient de frottement
R’
Nous voyons bien sur les deux figures que R est plus important que R’ d’un facteur 10 environ. Dans une première approximation, nous pouvons considérer le frottement dans notre code comme linéaire et le comparer à des frottements linéaires obtenus par d’autres méthodes. Ainsi Church et al. [2000] ont déduit une carte du coefficient de frottement sur le fond océanique (Figure 98) à partir de la dissipation globale déduite du modèle FES99 (Church, communication personnelle, 2000).
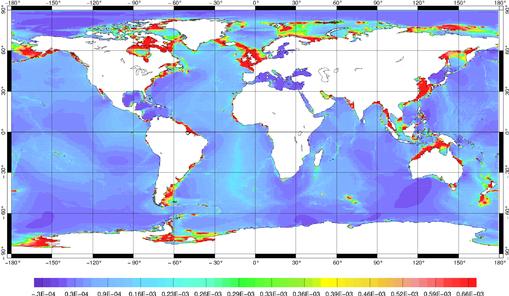
Figure 98 : Coefficient de frottement
linéaire calculé par Church et al.
La Figure 96 comparée à la Figure 98 rend bien compte de la trop faible valeur de notre coefficient de frottement R en particulier en plein océan où les différences peuvent atteindre un facteur 100. Par quoi peuvent donc s’expliquer ces différences ? Dans notre modélisation des marées, nous ne prenons en compte que les vitesses de la marée barotrope. Or, nous ne tenons pas compte de l’effet barocline de la marée alors que la génération d’ondes internes due à l’effet barocline n’est pas à négliger [Munk, 1997; Ray and Mitchum, 1996]. Les vitesses de marée doivent donc être moins importantes que celles que nous calculons dans CEFMO. Les coefficients de frottement sont donc sous estimés. Il est cependant difficile de dire de combien est cette sous estimation. Le facteur 100 n’est-il pas trop élevé ?
Nous avons voulu estimer ce facteur en utilisant dans notre code les coefficients de frottement déduits par Church et al. Le champ de Church et al. est limité aux zones de grands fonds et aux zones non polaires. C’est pourquoi, nous avons remplacé notre coefficient R calculés précédemment pour obtenir les dénivellations libres de FES2000, par ce nouveau champ de frottement sur tous les fonds de profondeurs plus importantes que 500 m et dans les zones polaires. De ce nouveau champ de frottement, nous avons déduit des vitesses à partir de nos solutions libres en dénivellation. Mais la simple technique de recollement des deux champs de frottement que nous avons mis en place, pose des problèmes de raccordement (pas de continuité) entre ces deux champs. C’est pourquoi les calculs que nous avons effectués sont entachés d’erreurs numériques trop importantes pour pouvoir faire des comparaisons plus avancées. Par manque de temps nous n’avons pas pu pousser plus loin nos investigations dans cette voie.